2次関数の変域を簡単に判断する方法

オンライン塾始めました。

６ヶ月で自分で勉強できるようにサポートします。

2017年9月15日2017年12月29日二次関数

[mathjax]

こんな問題があったとします。
関数y=x²の変域が-2≦x≦3のとき、
ｙの変域を求めよ。
図を書いてみると以下になります。

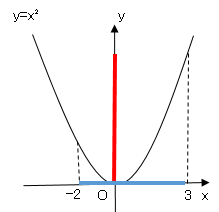
これより0≦y≦9となります。
しかし、図をいちいち書いているとそれだけで時間がかかってしまいます。

そこでポイント

「xの変域が負から正までのとき、
必ず0以上となり、どこまでかはxの両辺を代入して大きい方までとなります。」

上の例だと
変域が-2≦x≦3なので、
必ず0以上で、
x=-2のとき、y=4
x=3のとき、y=9
なので
0≦y≦9
となる。

テクニックを使うのは内容を理解してからでないと、ただの暗記になるので理解してから使いましょう。
不明点があればコメント欄よりお願いします。