関数の動点と面積の関係

問題１４

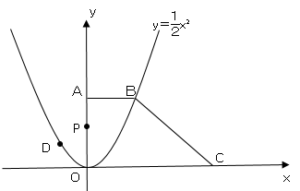
図のように、関数$y=\displaystyle \frac{x²}{2}$・・・①のグラフと台形$OABC$がある。
点$A,C$の座標はそれぞれ$(0,8)$,$(16,0)$である。点$B,D$は➀のグラフ上にあり、$B$の$x$座標は$4$,$D$の$x$座標は$-2$である。
また、点$P$は原点$O$を出発し、毎秒$1cm$の速さで、辺$OA,AB,BC$上を$C$まで動く。
ア、関数$y=\displaystyle \frac{x²}{2}$において、$x$の変域が$-6≦x≦4$のとき、$y$の変域を求めよ。
イ、直線$DP$が直線$OB$と平行になるのは、$P$が原点$O$を出発してから何秒後と何秒後か、求めなさい。
ウ、△$OPC$の面積が、台形$OABC$の面積の$\displaystyle \frac{1}{3}倍$になるときの$P$の座標をすべて求めなさい。

ア、
$2$次関数で$x$の変域が負から正に変わるので、必ず$0$を通ることがわかる。
$x=-6,4$を比べた時に$x=-6$の方がy座標が大きい。
$x=-6$を$y=\displaystyle \frac{x²}{2}$に代入して$y=18$よって$0≦y≦18$

イ、
直線$DP$が直線$OB$と平行になるとは、直線$DP$と$OB$の傾きが同じである。
点$B$の座標を求める。$B$の$x$座標は$4$なので、関数$y=\displaystyle \frac{x²}{2}$に代入して、
$y=\displaystyle \frac{4²}{2}$
$y=8$
よって点$B(4,8)$
点$D$の座標を求める。$D$の$x$座標は$-2$なので、関数$y=\displaystyle \frac{x²}{2}$に代入して、
$y=\displaystyle \frac{(-2)²}{2}$
$y=2$
よって点$D(-2,2)$

次に直線$OB$の式は$y=ax$に点$B$の座標を代入して
$8=4a$
$a=2$よって直線$OB$の式は$y=2x$



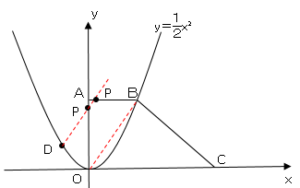
直線$DP$は図のように$2$か所で交わることがわかる。
➀点$P$が$OA$上のとき、$P$の$y$座標を$a$とすると$P(0,a)$と表すことができる。
このときの直線$DP$の傾きは$\displaystyle \frac{a-2}{0-(-2)}$

傾きが等しいので、
$2=\displaystyle \frac{a-2}{0-(-2)}$
$2=\displaystyle \frac{a-2}{2}$
$4=a-2$
$a=6$
よって$6$秒後
②点$P$が$AB$上のとき、$P$の$x$座標を$b$とすると$P(b,8)$と表すことができる。
このときの直線$DP$の傾きは$\displaystyle \frac{8-2}{b-(-2)}$、傾きが等しいので、
$2=\displaystyle \frac{6}{b+2}$
$2(b+2)=6$
$2b+4=6$
$b=1$
よって$9$秒後

ウ、
まず台形$OABC$の面積を求める。
$(AB+OC)×AO÷2$
$=(4+16)×8÷2$
$=80$よって△$OPC$の面積は$\displaystyle \frac{80}{3}$
ここで$OPC$の面積は底辺を$OC$とすると高さが変化することがわかる。
$AB$上に点$P$がある場合は高さが一定であり、その面積は$16×8÷2=64$となり誤り。
可能性があるのは点$P$が$OA$上か$BC$上にあるときである。

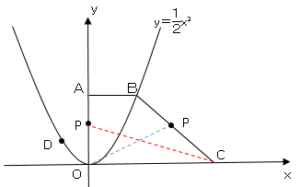
高さを$P$とすると、△$OPC$の面積は
$16×p÷2$
$=8p$
これが$\displaystyle \frac{80}{3}$になるので、
$8p=\displaystyle \frac{80}{3}$
$p=\displaystyle \frac{10}{3}$

高さが$\displaystyle \frac{10}{3}$となる。
➀点$P$が$OA$上にある場合Pの座標は$P(0,\displaystyle \frac{10}{3})$
②点$P$が$BC$上にある場合直線$BC$を求める。
$1$次関数$y=ax+b$に点$B,C$の値を代入
$\begin{equation}\begin{cases}\; 8=4a+b･･･① \\\; 0=16a+b･･･②\end{cases}\end{equation}$
➀-②より
$8=-12a$
$a=-\displaystyle \frac{2}{3}$･･･③
③を②に代入して
$0=16×(-\displaystyle \frac{2}{3})+b$
$b=\displaystyle \frac{32}{3}$
これより直線$BC$は$y=-\displaystyle \frac{2x}{3}+\displaystyle \frac{32}{3}$

$P$の$y$座標は$\displaystyle \frac{10}{3}$なので、直線$BC$の式に代入して、
$\displaystyle \frac{10}{3}=-\displaystyle \frac{2x}{3}+\displaystyle \frac{32}{3}$
$10=-2x+32$
$-22=-2x$
$x=11$
$P$の座標は$P(11,\displaystyle \frac{10}{3})$