関数で垂線の傾きを求める簡単な方法

オンライン塾始めました。

６ヶ月で自分で勉強できるようにサポートします。

2017年9月16日2017年12月29日一次関数, 二次関数

[mathjax]

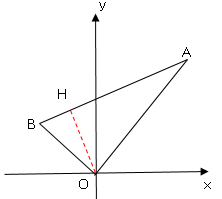
こんな問題があったとします。
3点O(0,0),A(2,4),B(-1,2)を結んでできた三角形があるとする。底辺をABとしたときの高さOHのHの座標を求めなさい。

普通にやると➀三角形OABの面積を求めて、②三平方の定理でABを求めて、③三角形OAB面積＝AB×OH÷2でOHの長さを求めて、④Hの座標をaなどで置いて求めます。

しかし、➀から④をすべてやると時間がかかります。

そこでポイント

「ABの傾き×OHの傾き＝-1という公式を使います。条件はABとOHの角度が直角の場合です。（中学校では習いません・・・）」

上の例だと
ABの傾きはy=ax+bに点A,Bの座標を代入して、連立方程式を解いて、
\[y=\frac{2x}{3}+\frac{8}{3}となる。\]
ポイントより
\[\frac{2}{3}×OHの傾き＝-１\]\[OHの傾き＝\frac{-3}{2}\]\[これよりOHの式はy=\frac{-3x}{2}となる。\]
Hの座標は直線AB,OHの式を連立して、\[(\frac{-16}{13},\frac{24}{13})\]となる。

テクニックを使うのは内容を理解してからでないと、ただの暗記になるので理解してから使いましょう。
不明点があればコメント欄よりお願いします。