関数において最短距離を求めるコツは対称移動。

オンライン塾始めました。

６ヶ月で自分で勉強できるようにサポートします。

2017年9月27日2017年12月29日一次関数, 二次関数

[mathjax]

こんな問題があったとします。直線➀はy=2x+1、点Aは直線➀上の点でAの座標は(3,7)である。x軸の交点をE(2,0)とする。y軸上に点FをAF+FEの長さが最も短くなるようにとるとき、点Fのy座標を求めよ。

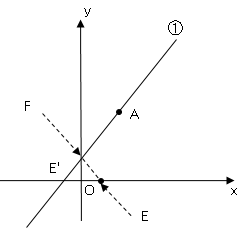
考え方：「点Eをy軸に対象移動させた点E’と点Aとを結んだ直線とy軸との交点にFがあると考える」。
つまり「直線AE’の切片が求める点Fのy座標となる」
\[1次関数y=ax+bに\]\[点A(3,7),E'(-2,0)の値を代入\]\begin{equation}\begin{cases}\; 7=3a+b･･･① \\\; 0=-2a+b･･･②\end{cases}\end{equation}\[これより\]\[b=\frac{14}{5}\]\[ゆえに点Fのy座標は\frac{14}{5}\]

テクニックを使うのは内容を理解してからでないと、ただの暗記になるので理解してから使いましょう。
不明点があればコメント欄よりお願いします。