度数分布票の細かい指示を読み取れるかの問題

問題１２表はある工場で使われているネジを作る機械A、B、Cの性能を確かめるためにそれぞれの機械によって、1時間で作られたネジの一本あたりの重さを度数分布表にまとめたものである。

なおこの工場では4.8g以上5.2g未満のネジを合格品としている。表から分かることについて正しく述べたものを全て選びなさい。
 
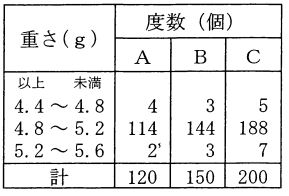
ア、1時間あたりで、合格品を最も多く作ることができる機械はAである。
イ、1時間あたりで、合格品を最も多く作ることができる機械はBである。
ウ、1時間あたりで、合格品を最も多く作ることができる機械はCである。
 
エ、1時間辺りで合格品を作る割合が最も高い機械はAである。
オ、1時間辺りで合格品を作る割合が最も高い機械はBである。
カ、1時間辺りで合格品を作る割合が最も高い機械はCである。
 
キ、1時間あたりで作ったネジの重さの平均値が5gより小さくなる機械はAである。
ク、1時間あたりで作ったネジの重さの平均値が5gより小さくなる機械はBである。
ケ、1時間あたりで作ったネジの重さの平均値が5gより小さくなる機械はCである。

方針

1時間当たり合格品を多く作っているのはCなので、ウ
 
1時間辺りで合格品を作る割合はそれぞれ計算して求める。1時間に作れるねじの個数が違うので。
A:$\displaystyle \frac{114}{120}$
B:$\displaystyle \frac{144}{150}$
C:$\displaystyle \frac{188}{200}$
計算してもいいがめんどうなので・・・分母を600(最小公倍数)に統一する。
 
A:$\displaystyle \frac{570}{600}$
B:$\displaystyle \frac{576}{600}$
C:$\displaystyle \frac{564}{600}$
これより分子の数が一番多いBとなり、オ
 
A,B,Cの平均値を求めると
A:$\displaystyle \frac{4×4.6+114×5+2×5.4}{120}$
B:$\displaystyle \frac{3×4.6+144×5+3×5.4}{150}$
C:$\displaystyle \frac{5×4.6+188×5+7×5.4}{200}$
 
これを計算してでもいいが、工夫すると
合格品が5gとなるのでそれを除く値で平均値を求めて考えたほうが楽。よって
 
A:$\displaystyle \frac{4×4.6+2×5.4}{6}$
B:$\displaystyle \frac{3×4.6+3×5.4}{6}$
C:$\displaystyle \frac{5×4.6+7×5.4}{12}$
 
それぞれ計算すると
a:4.8・・・、b:5、c:5.06・・・
これよりキ
まとめるとウ、オ、キ