ヒストグラムに生徒を付け足し、考える問題
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
2860 Views
問題11A中学校のバスケットボール部はある日の練習で、全ての部員がそれぞれシュートを5回ずつ行い、成功した回数を記録した。図はその記録をもとに、成功した回数別の人数をグラフに表したものである。
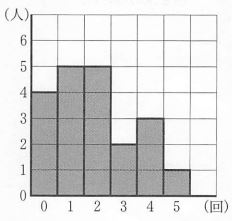
ヒストグラムに生徒を付け足し、考える問題
(2)図から成功した回数の平均値を求めなさい。
(3)バスケットボール部に入部を予定している花子さんも、別の日にシュートを5回行い成功した回数を記録した。花子さんの記録を図に表された記録に加え、成功した回数の平均値と中央値を求めると二つの値が等しくなった花子さんの成功した回数を求めなさい。

(2)図から成功した回数の平均値を求めなさい。
(3)バスケットボール部に入部を予定している花子さんも、別の日にシュートを5回行い成功した回数を記録した。花子さんの記録を図に表された記録に加え、成功した回数の平均値と中央値を求めると二つの値が等しくなった花子さんの成功した回数を求めなさい。
方針
ヒストグラムからデータを小さい順に戻して考える。
図より以下のデータのようになる。
(1)
図から0点の人は4人いる、1点の人は5人・・・すると以下のように並べられる。
0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,4,4,4,5
よってバスケ部の人数は4+5+5+2+3+1=20人
(2)
平均値は得点の合計を人数で割る。
$\displaystyle \frac{1×5+2×5+3×2+4×3+5×1}{20}=$1.9
(3)
花子さんを入れる前の中央値は10番目の2と11番目の2の平均値で2。
花子さんの点数をa点とすると中央値は11番目の値になるが、そもそも「花子さんを入れる前の10番目,11番目,12番目は2になっている」ので、花子さんをいれたあとも中央値は2になる。
具体的に考えてみると
2より前にa(0,1点)を入れても中央値は2
0,0,0,0,1,1,a,1,1,1,2,2,2,2,2,3,3,4,4,4,5
2のところにa(2点)を入れても中央値は2
0,0,0,0,1,1,1,1,1,2,2,2,2,a,2,3,3,4,4,4,5
2より後にa(3,4,5点)を入れても中央値は2
0,0,0,0,1,1,a,1,1,1,2,2,2,2,2,3,3,a,4,4,4,5
これより花子さんを入れた後の平均値と中央値を求めると二つの値が等しいので、
$\displaystyle \frac{1×5+2×5+3×2+4×3+5×1+a}{21}=2$
$\displaystyle \frac{38+a}{21}=2$
$38+a=42$
$a=4$
よって花子さんの成功した回数は4回
不明点があればコメント欄よりお願いします。





ディスカッション
コメント一覧
まだ、コメントがありません