カードの和と積の関係

問題４$1$から$8$までの自然数が書いてある$8$枚のカードがあります。
この箱から同時に$2$枚のカードを取り出し、その積を$a$とする。
残りの$6$枚のカードの和を$b$とする。
このとき、$a+b$の和が$40$より大きい偶数になる確率を求めましょう。

方針

先に$2$枚選べば、自動的に残りの$6$枚は決まる。
全体の母数は$8×7=56$通りだが、
先に選んだ$2$枚の中に$(1,2)$と$(2,1)$が含まれるがこれは重複している。
よって母数は$56÷2=28$
ごり押ししてもかまわないが、工夫するやり方で解説します。

$1$から$8$までの和は$36$
最初に選んだ数を$x,y$とすると、以下の不等式がなりたちます。
$x×y+36-x-y>40$
$xy-x-y>4$
問題は$42$以上にしたいので、
$xy-x-y≧6$
これを満たす数を選べばよい。

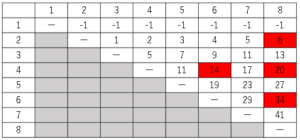
グラフより求める確率は
$\displaystyle \frac{4}{28}$
$=\displaystyle \frac{1}{7}$