サイコロとグラフの関係
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
7399 Views
問題５大小$2$つのサイコロを同時に投げる。
大きいサイコロの出た目の数を$a$、小さいサイコロの出た目の数を$b$とする。
（１）$\displaystyle \frac{b}{a}=2$となる確率を求めましょう。
（２）$2$直線$y=\displaystyle \frac{b}{a}x,y=-x+8$の交点の$x$座標、$y$座標が共に自然数となる確率を求めましょう。
（３）$3$直線$y=\displaystyle \frac{b}{a}x,y=\displaystyle \frac{a}{b}x,y=-x+8$で囲まれる三角形の内部に半径$\sqrt{2}cm$の円をかくことができる$a,b$の組み合わせは何通りありますか。ただし座標軸の単位の長さは$1cm$とする。
大きいサイコロの出た目の数を$a$、小さいサイコロの出た目の数を$b$とする。
（１）$\displaystyle \frac{b}{a}=2$となる確率を求めましょう。
（２）$2$直線$y=\displaystyle \frac{b}{a}x,y=-x+8$の交点の$x$座標、$y$座標が共に自然数となる確率を求めましょう。
（３）$3$直線$y=\displaystyle \frac{b}{a}x,y=\displaystyle \frac{a}{b}x,y=-x+8$で囲まれる三角形の内部に半径$\sqrt{2}cm$の円をかくことができる$a,b$の組み合わせは何通りありますか。ただし座標軸の単位の長さは$1cm$とする。
方針
サイコロ$2$つは表を書いて数えた方が早くて確実。
表を書いて答えを求める。
（１）
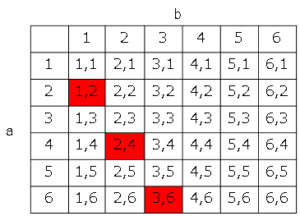
これより、求める確率は
$\displaystyle \frac{3}{36}$
$=\displaystyle \frac{1}{12}$
$y=-x+8$の交点となる座標を調べる。
（２）
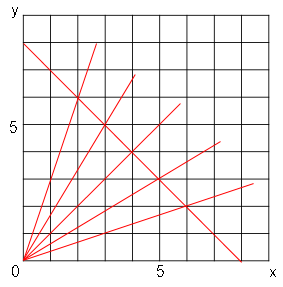
交点の座標は以下のようになります。
・$(2,6)$
・$(3,5)$
・$(4,4)$
・$(5,3)$
・$(6,2)$
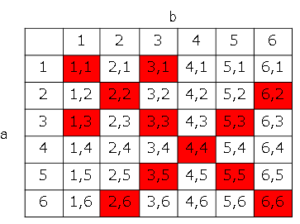
これより求める確率は
$\displaystyle \frac{12}{36}$
$=\displaystyle \frac{1}{3}$
半径$\sqrt{2}$なので実際書いてみる。
（３）
実際の図をコンパスなどで書くとわかり易いです。
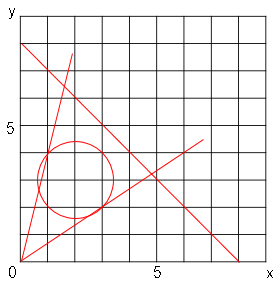
この円が入る点をそれぞれ求めればよい。
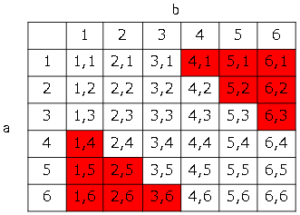
これより$12$通りとなる。
不明点があればコメント欄よりお願いします。