立体の体積の求め方の工夫
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
4807 Views
問題21図のような1辺の長さが3cmである立方体ABCDEFGHがある。辺BF上にBP=2cmとなる点P、辺FE上にFQ=2cmとなる点Q、辺FG上にFR=2cmとなる点Rをとる。
➀線分DPの長さを求めなさい。
②四角錘BAQRCの体積を求めなさい。
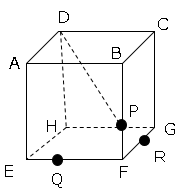
➀線分DPの長さを求めなさい。
②四角錘BAQRCの体積を求めなさい。

方針
長さはまず三平方の定理を考えてみる。
次に相似を考えてみる。
体積は色々延長して線を引くとうまくいくことが多い。
➀
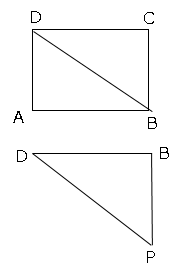
上の図で△ABDに3平方の定理を用いて
DB²=DA²+AB²=18
BPの長さは2
また下の図で△PBDに3平方の定理を用いて
$DP²=DB²+BP²$
$DP²=18+4$
$DP=\sqrt{22}$
②
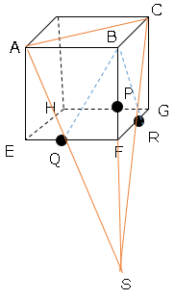
以下のように補助線をひき点Sとおく。
四角錘BAQRCの体積は
(S-BAC)ー(Q-BSR)となる。
S-BACの体積を求める。
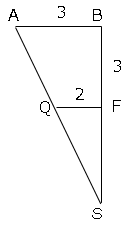
三角形の図より
△SFQ∽△SAB
よって$FS$の長さを$x$とおくと
$FQ:AB=FS:SB$
$2:3=x:x+3$
$3x=2x+6$
$x=6$
よって
$BS=3+6=9$
S-BACの体積は
$=3×3÷2×9÷3$
$=\displaystyle \frac{27}{2}$
Q-BSRの体積を求める。
$9×2÷2×2÷3=6$
四角錘BAQRCの体積は(S-BAC)-(Q-BSR)
$=\displaystyle \frac{27}{2}-6$
$=\displaystyle \frac{15}{2}cm³$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません