半分の面積の考え方

問題９関数$y＝-\displaystyle \frac{1}{4}x²$・・・①のグラフ上に、２点Ａ，Ｂがあります。点Ａのｘ座標を－８、点Ｂのｘ座標を４とします。点Ａ、Ｂを通る直線とｙ軸との交点を点Ｃとする。次の問いに答えよ。
１.点Ａのｙ座標を求めよ。
２.点Ａ、Ｂを通る直線の式を求めよ。
３. △ＯＡＢの面積を求めよ。
４.点Ｑを△ＯＡＢ上の辺上にとり、線分ＣＱが△ＯＡＢの面積を２等分するとき、点Ｑの座標を求めなさい。

方針

面積の話なので、各点の座標を求める。
わからない場合は文字で置く。

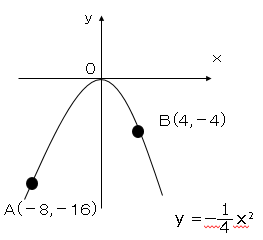
１.
➀のグラフにｘ＝－８を代入して、点Ａ（－８,－１６）

２.
➀のグラフにｘ＝４を代入して、点Ｂ（４,－４）
よって直線ＡＢはｙ＝ｘ－８となる。
（２点Ａ，Ｂが出ているのでｙ＝ａｘ＋ｂに代入して計算）

３.

直線ＡＢとｙ軸との交点をＣなので、Ｃ＝（０,－８）となる。
よって三角形ＯＡＢの面積は
△ＯＣＡ＋△ＯＣＢ
８×８÷２＋８×４÷２＝４８

４.

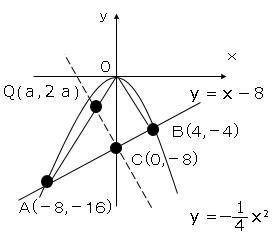
直線ＡＯの式は
（点Ａが出ているのでｙ＝ａｘに代入して計算）
ｙ＝２ｘ
Ｑのｘ座標をａとするとｙは２ａとなる。

よってＱの座標はＱ（ａ,２ａ）（ａ＜０）

３より
△ＯＡＢの面積は４８
よって四角形ＯＢＣＱの面積は２４となる。
四角形ＯＢＣＱ＝△ＯＣＱ＋△ＯＣＢなので
２４＝４×ａ÷２＋４×４÷２
ａ＝２

よってＱの座標は（－２、－４）