タイルと被りの関係
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
7638 Views
問題17同じ大きさの黒、白、赤の3色のタイルがある。これらを使って、図1の1番目、2番目、3番目、・・・のように、規則的に並べて図形を作る。また、それぞれ図形について、黒、白、赤の色ごとにタイルの枚数を調べ、下のような表をつくる。
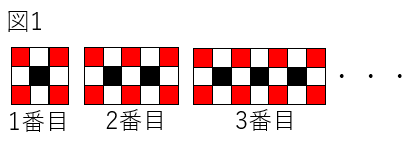
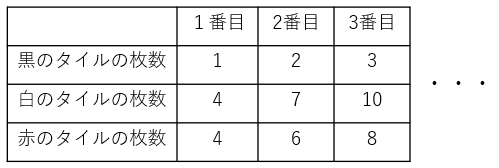
(1)4番目の図形の黒、白、赤のタイルの枚数をそれぞれ求めなさい。
(2)$n$番目の図形の白のタイルの枚数を$n$を使って表しなさい。
(3)並べたすべてのタイルの枚数が99枚になるのは、何番目の図形か。
(4)10番目の図形を作ったあと、縦方向にも同じように規則的に並べて、図2のように、黒タイルが横に10枚、縦に5枚、合計50枚となるような図形を作った。このとき、使った白いタイルの枚数を求めよ。
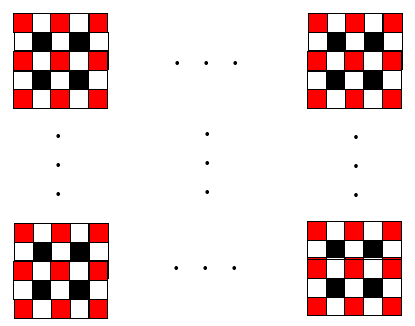


(1)4番目の図形の黒、白、赤のタイルの枚数をそれぞれ求めなさい。
(2)$n$番目の図形の白のタイルの枚数を$n$を使って表しなさい。
(3)並べたすべてのタイルの枚数が99枚になるのは、何番目の図形か。
(4)10番目の図形を作ったあと、縦方向にも同じように規則的に並べて、図2のように、黒タイルが横に10枚、縦に5枚、合計50枚となるような図形を作った。このとき、使った白いタイルの枚数を求めよ。

方針
黒・白・青のタイルの枚数をそれぞれ規則的に表す。
$n$番目まで出してみる。
(1)
黒のタイルの枚数は
$1$番目は$1$枚
$2$番目は$2$枚
$3$番目は$3$枚
・・・
$n$番目は$n$枚
白のタイルの枚数は(2番目は1番目の白タイルに3枚足したもの。3番目は2番目の白タイルに3枚足したもの。)
$1$番目は$4(=4+0×3)$枚
$2$番目は$7(=4+1×3)$枚
$3$番目は$10(=4+2×3)$枚
・・・
$n$番目は$3n+1(=4+(n-1)×3)$枚
赤のタイルの枚数は(2番目は1番目の赤タイルに2枚足したもの。3番目は2番目の赤タイルに2枚足したもの。)
$1$番目は$4(=4+0×2)$枚
$2$番目は$6(=4+1×2)$枚
$3$番目は$8(=4+2×2)$枚
・・・
$n$番目は$2n+2(=4+(n-1)×2)$枚
これより4番目のタイルの枚数はそれぞれ
黒:4枚、白:13枚、赤:10枚
(2)
(1)より$3n+1$枚
(3)
$n$番目のすべてのタイルの枚数は(1)の黒、白、赤のタイルの枚数を足して、
$n+3n+1+2n+2$
$=6n+3$
これが$99$枚になるので、
$6n+3=99$
$6n=96$
$n=16$
よって$16$番目
被る範囲を探し、何枚被るか考えてみる。
(4)
1段目の白のタイルの枚数は$3n+1$に$n=10$を代入してより31枚
2段目も白のタイルの枚数は31枚何だが、
1段目と2段目で白のタイルが一部被ってしまっている。
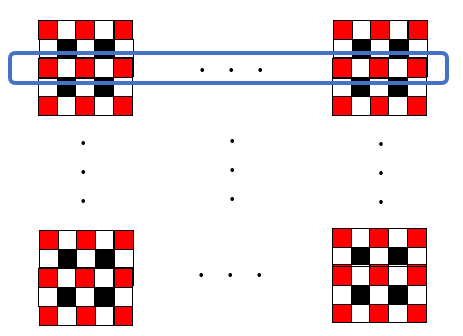
被っている枚数は$1×10$で10枚となる。
よって白いタイルの枚数は
$31+21×4$(1段目(31)+4段被るので(21×4))
$=115$
$115$枚となる。
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません