関数と面積比

問題１２

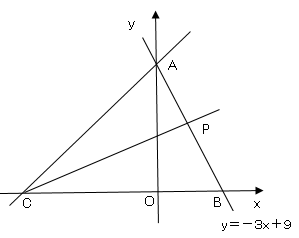
図で点$O$は原点、直線$ℓ$は$1$次関数$y=-3x+9$のグラフを表している。
直線$ℓ$と$y$軸との交点を$A$、直線$ℓ$と$x$軸との交点を$B$とする。
直線$ℓ$上にある点を$P$とする。
点$P$の$x$座標が$0≦x≦3$であるとき、$x$軸上にあり、$x$座標が$-12$である点を$C$とし、点$A$と点$C$を結び、$2$点$C,P$を通る直線を$m$とした場合
ア、直線$m$が△$ACB$の面積を$2$等分するときの直線$m$の式を求めよ。
イ、$y$軸を対称の軸として点$B$と線対称な点を$D$とし、点$D$と点$P$を結ぶ。
△$CDP$の面積が△$ACP$の面積の$\displaystyle \frac{2}{5}$倍のとき、点$P$の$x$座標を求めよ。

ア、
△$ACP$の底辺を$AP$とし、△$BCP$の底辺を$BP$とすると、高さは共通になる。
よって、点$P$が線分$AB$の中点にあればよい。
よって点$P$の座標は
$(\displaystyle \frac{3-0}{2},\displaystyle \frac{9-0}{2})$
$(\displaystyle \frac{3}{2},\displaystyle \frac{9}{2})$
点$P$の座標は$(\displaystyle \frac{3}{2},\displaystyle \frac{9}{2})$

直線$m$を求める。$1$次関数$y=ax+b$に点$P,C$の値を代入
$\begin{equation}\begin{cases}\; \displaystyle \frac{9}{2}=\displaystyle \frac{3}{2}a+b･･･① \\\; 0=-12a+b･･･②\end{cases}\end{equation}$
②-➀より
$-\displaystyle \frac{9}{2}=-12a-\displaystyle \frac{3}{2}a$
$-9=-24a-3a$
$27a=9$
$a=\displaystyle \frac{1}{3}$･･･③
③を②に代入して
$0=-4+b$
$b=4$
これより直線$AB$は$y=\displaystyle \frac{x}{3}+4$

イ、


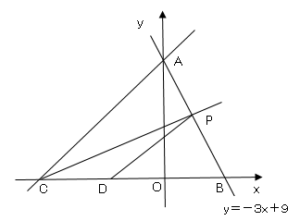
点$D$の座標は$(-3,0)$△$CDP$と△$DBP$は高さが共通なので、辺の比が面積比になる。
よって
△$CDP:△DBP=9:6=3:2$
△$DBP$の面積は$\displaystyle \frac{2}{3}$△$CDP$

△$ACP$の面積は△$ABC$の面積-△$CDP$-△$DBP$で求められる。

△$ABC$の面積は$9×15÷2=\displaystyle \frac{135}{2}$

よって△$ACP$の面積
$\displaystyle \frac{135}{2}$-△$CDP$-$\displaystyle \frac{2}{3}$△$CDP$
$=\displaystyle \frac{135}{2}-\displaystyle \frac{5}{3}$△$CDP$

△$CDP$の面積が△$ACP$の面積の$\displaystyle \frac{2}{5}$倍なので
△$CDP=(\displaystyle \displaystyle \frac{135}{2}-\displaystyle \frac{5}{3}$△$CDP)×\displaystyle \frac{2}{5}$
△$CDP=27-\displaystyle \frac{2}{3}$△$CDP$
$\displaystyle \frac{5}{3}$△$CDP=27$
△$CDP=\displaystyle \frac{81}{5}$

点$P$の$x$座標を$a$とすると$y$座標は$-3a+9$となる。
よって△$CDP$の面積は
$9×(-3a+9)÷2=\displaystyle \frac{81}{5}$
$-3a+9=\displaystyle \frac{18}{5}$
$-3a=\displaystyle \frac{18}{5}-9$
$-3a=-\displaystyle \frac{27}{5}$
$a=\displaystyle \frac{9}{5}$
点$P$の$x$座標は$\displaystyle \frac{9}{5}$