代表値と散らばり
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
6704 Views
階級値と範囲
資料の最大の値と最小の値の差を、分布の範囲（レンジ）という。
次の例（1,2,3,4,5,6,7,8,9）だと範囲は８
度数分布表で各階級の真ん中の値を階級値という。
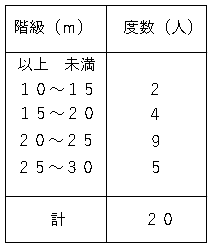
１例を考えると、１０以上１５未満の場合は階級値は１２.５となる。
では問題です。上記の表の２０以上２５未満の階級値を求めましょう。
さまざまな代表値
資料の値の総和を、資料の個数で割ったものを平均値と呼び、以下の式で表される。
$平均値=\displaystyle \frac{(階級値)×(度数)}{(度数の合計)}$
資料の値を大きい順にならべたときの中央の値を中央値（メジアン）と呼ぶ。
※資料の個数が偶数の場合は中央２個の平均を中央値とする。1,2,3,4,5,6,7,8,9,10
この場合の２個の中央値は５.５（$\displaystyle \frac{5+6}{2}$）となる。
資料の中で最も多く現れる数字を最頻値（モード）と呼ぶ。
10,2,3,4,4,5,6,6,8,9,10,2,4
この場合の最頻値は４となる。
では問題です。表はあるテストの結果である。以下の問いに答えてみましょう。
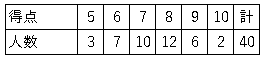
（１）中央値を求めましょう。
（２）最頻値を求めましょう。
（２）平均値を求めましょう。
不明点があればコメントよりどうぞ。