円とおうぎ形の特徴
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
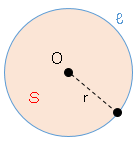
円の弧と弦について
円周上に$2$点$A,B$をとるとき、円周の$A$から$B$までの部分を、弧(こ)$AB$と言いと書きます。$\stackrel{ \Large \frown }{ AB }$と書きます。また、$\stackrel{ \Large \frown }{ AB }$の両端の点を結んだ線分を、弦(げん)$AB$といいます。
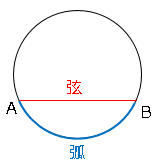
注：図の上側も弧$AB$になりますが、ここでは説明のため省略。
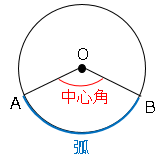
円と中心角
図の∠$AOB$を$\stackrel{ \Large \frown }{ AB }$に対する中心角と言います。
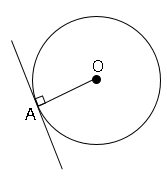
円と接線と接点
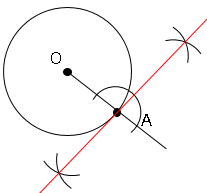
円と直線が１点で交わるときに、直線は円に接するといい、その直線を接線、接する点（図の点$A$）を接点と言います。さらに特徴として円の接線は、その接点を通る半径に垂直である。
意味を理解したら問題を解いてみましょう。
図の円で点Ａを接点とする接線を書きましょう。
おうぎ形の特徴
ピザのような図形をおうぎ形と言います。半径が作る角を中心角と言います。
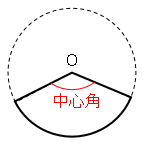
円を書いた理由はおうぎ形は円の一部だからです。
円とおうぎ形の周の長さと面積
半径$r$で円の周の長さを$ℓ$、円周率を$π$、円の面積を$S$とすると、
円の周の長さ：$ℓ=2πr$
円の面積：$S=πr²$
半径$r$で、中心角を$a°$、円周率を$π$、おうぎ形の弧の長さを$ℓ$、おうぎ形の面積を$S$とすると、
弧の長さ：$ℓ=2πr×\displaystyle \frac{a}{360}$
おうぎ形の面積：$S=πr²×\displaystyle \frac{a}{360}$
※中学生の場合：円周率(3.14・・・)は$π$になります。
ここで注目してほしいのはおうぎ形の面積と弧の長さは円周と円の面積に$\displaystyle \frac{a}{360}$をかけたものになります。これは円の一部がおうぎ形だからです。$a=360°$の場合は円になります。
さらに発展させて、
$ℓ=2πr×\displaystyle \frac{a}{360}$、$S=πr²×\displaystyle \frac{a}{360}$なので、
$S=πr²×\displaystyle \frac{a}{360}$(両辺を$2$かけて、$r$で割ると)
$\displaystyle\frac{2S}{r}=$$2πr×\displaystyle \frac{a}{360}$
$\displaystyle\frac{2S}{r}=ℓ$
$S=$の形にすると
$S=\displaystyle\frac{ℓr}{2}$
となり中心角がわからなくても弧の長さとおうぎ形の半径がわかれば面積を求められます。
では問題を解いてみましょう。
半径$6cm$、弧の長さが$8πcm$のおうぎ形の中心角と面積を求めなさい。
不明点があればコメントよりどうぞ。