マス目と移動の仕方の問題
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
6085 Views
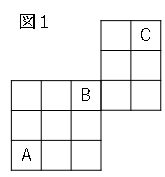
問題7図$1$のように、数字を記録するためのマス目があり、マス目中の$A$から$B$を通り、$C$まで数字を記録しながら移動することにする。
ただし、移動の仕方は、右または上に$1$マスずつ移動するとし、右に移動するときは、移動前のマス目に記録された数に$1$を加えた数を移動後のマス目に記録する。
また、上に移動するときは、移動前のマス目に記録された数を$2$倍した数を記録後のマス目に記録する。
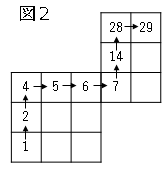
例えば、図$2$のような場合を考える。
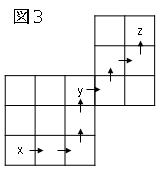
(1)図$3$のように移動するとき、$x=3$のとき、$y,z$の値を求めましょう。
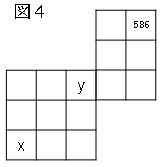
(2)図$4$のように、$z=586$のとき、$x$の値を求めましょう。
(3)$x$の値は同じでも、移動の仕方により値は異なる。
$x$の値が同じとき、$z$が最も大きくなる数から最も小さくなる数をひいた差を求めましょう。
ただし、移動の仕方は、右または上に$1$マスずつ移動するとし、右に移動するときは、移動前のマス目に記録された数に$1$を加えた数を移動後のマス目に記録する。
また、上に移動するときは、移動前のマス目に記録された数を$2$倍した数を記録後のマス目に記録する。

例えば、図$2$のような場合を考える。

(1)図$3$のように移動するとき、$x=3$のとき、$y,z$の値を求めましょう。

(2)図$4$のように、$z=586$のとき、$x$の値を求めましょう。

(3)$x$の値は同じでも、移動の仕方により値は異なる。
$x$の値が同じとき、$z$が最も大きくなる数から最も小さくなる数をひいた差を求めましょう。
方針
規則を正確に読み取る。
規則に従う
(1)
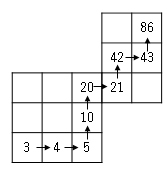
図より、$y=20,z=86$
$2$で割りきれるときは、それに従う
(2)
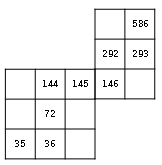
図より、$x=35$
最大・最小になるパターンをそれぞれ考える。
(3)
・最小は先に$2$倍してから足す。
・最大は先に足してから$2$倍する。
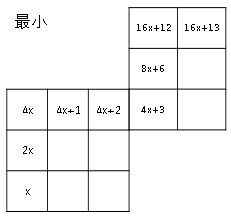
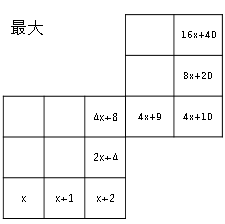
これより
$16x+40-(16x+13)$
$=27$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません