平面図形の練習問題１
LINE@始めました。
友達追加をよろしくお願い申し上げます。
勉強のやり方の相談・問題の解説随時募集しています！
お気軽にＬＩＮＥしてください。
5869 Views
2018年3月16日平面図形中学１年生
問１
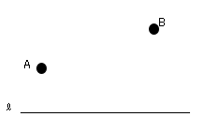
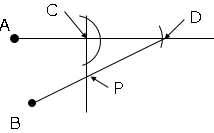
図の直線$ℓ$上にあり、$2$点$A,B$から等しい距離にある点$P$を作図しなさい。
考え方は実際に答えをフリーハンドで書きこんでみると以下の図になる。
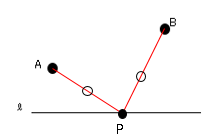
これを元に垂直二等分線か角の二等分線を用いて書く。
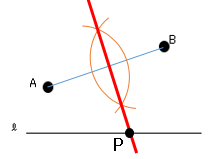
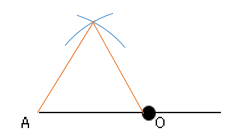
すると以下の図のように垂直二等分線を書く。
➀線分$AB$を描く。
➁点$A,B$から半円を描く。※半径は同じ
➂➁で書いた半円同士の交わった部分を結び、$ℓ$との交点が点$P$。
問２
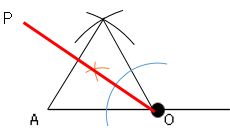
図で∠$POA$が次の大きさになるような直線$OP$を、直線$AO$の上側に作図しなさい。∠$POA=30°$
正三角形を描き、（角度が６０°）角の二等分線で半分の３０°を作る。
➀$AO$の長さをコンパスで計り、点$A$を軸に半円を、点$O$を軸に半円を描き交点を求め、点$A、O$を結ぶ
➁角の二等分線を描く。
問３
図のようなおうぎ形の弧の長さと面積を求めなさい。
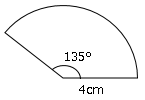
おうぎ形の周の長さは
$=8×π×\displaystyle \frac{135}{360}$
$=3πcm²$
おうぎ形の面積は
$=4×4×π×\displaystyle \frac{135}{360}$
$=6πcm²$
問４
図の影をつけた部分の面積を求めなさい。
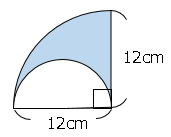
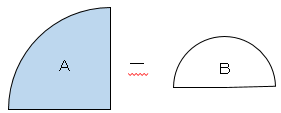
影の部分の面積はＡからＢを引いた残りとなる。
Ａの面積は
$12×12×π×\displaystyle \frac{90}{360}$
$=36πcm²$
Ｂの面積は
$6×6×π×\displaystyle \frac{180}{360}$
$=18πcm²$
影の部分の面積は
$36π-18π$
$=18πcm²$
問５
図で、直線$m$上にあり、折れ線$AP+PB$の長さが最短となるような点$P$を作図しなさい。
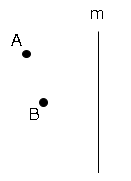
最短の問題は
直線となる。
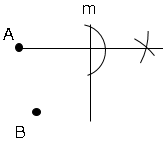
➀点$A$を直線$ｍ$に対して対象に移動させるために垂直二等分線を引く。
➁直線$ｍ$と➀の垂直二等分線との交点を$C$とし、その点を中心に半径が$AC$の長さの弧を描き、➀の垂直二等分線との交点を$D$とする。
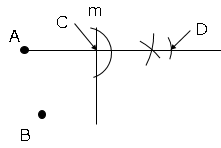
➂点$D$と$B$を結んで、$m$との交点を$P$とする。
不明点があればコメントよりどうぞ。