立体と空間図形
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
色々な立体
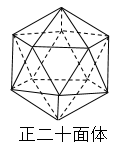
平面だけで囲まれた立体のことを多面体という。多面体のうちどの面もみな合同な正多角形、どの頂点にも面が同じだけ集まっているものを正多面体という。正多面体は以下の5種類しかない。
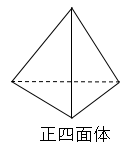
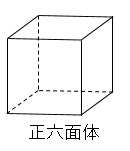
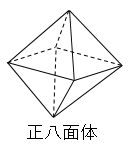
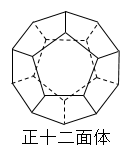

マサヤ君
先生平面って何ですか?

土屋先生
平面とは縦と横の世界で表したものだよ。例えば君たちがよく使っている「机の表面」は縦と横だね。つまり平面だよ。

学校の机は拡大するとこんな感じだね。他にも平面は色々あるよ。
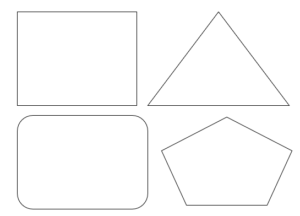
よ~く見てみると上にある5つの図形は平面でできている図だよね?わかるかな?

ユリコさん
わかった!正四面体は三角形が4個付いてできています。正六面体は四角形が6個ついています。正八面体は三角形が8個つています。正十二面体は五角形が〇〇個ついています(笑)

土屋先生
ごまかさないでね~(笑)正「四」面体は文字通り三角形が「4」個ついているね。正「六」面体は文字通り四角形が「6」個ついているね。正「八」面体は文字通り三角形が「8」個ついているね。さて推測してみよう。

ユリコさん
てことは正十二面体は五角形が12個、正二十面体は三角形が20個ですね。

土屋先生
よくできました!その通りです。

マサヤ君
先生、もしかして正〇〇面体とあるので・・・正四面体は「正」三角形が、正六面体は「正」方形(正四角形)が正八面体は「正」三角形で・・・構成されているってことですよね?!

土屋先生
するどいね!!そういうことだよ。じゃあ他の特徴も考えてみよう。辺、頂点の数はどうかな?まずは数えてみよう。

マサヤ君
正四面体の辺の数は6本で、頂点の数は4つです。
正六面体の辺の数は12本で、頂点の数は8つです。
正八面体の辺の数は12本で、頂点の数は6つです。
正十ニ面体の辺の数はわかりません。数えれるけど・・・面倒くさorz。

土屋先生
めんどくさいって思うことは悪くないんだよ!「工夫して考える第一歩目」を踏み出しだよ。だからめんどくさいから法則かなんか見つかればいいな~って思うのはものすごく大事だよ。先生も一回は数えたことあるけど、もうやらないね(笑)めんどくさいから(笑)

マサヤ君
そうしたら法則を考えてみよう!でもどうやって?

土屋先生
まずは辺について考えてみよう。正四面体を考えてみるよ。
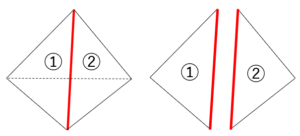
➀と➁の三角形に共通するのは赤の線だね。正四面体は正三角形が4つついたものだから辺の数は$3×4=12$(正三角形の辺の数×面の数)のはずだけど、ダブル部分(共通する部分)があるね。そのダブル部分をなくしてみよう。どうすればいいかね?

マサヤ君
1つの辺に対してダブル部分がある。今、全体で$12$本だから$÷2$をしてあげればダブル部分を取り除けます!!だから$12÷2=6$本ですね。

土屋先生
その通りだよ!今日はさえてるね!続けて他の辺も考えてみよう。

マサヤ君
正六面体の場合$4×6=24$本だけどダブりをなくすと、$24÷2=12$本。
正八面体の場合$3×8=24$本だけどダブりをなくすと、$24÷2=12$本。
正十二面体の場合$5×12=60$本だけどダブりをなくすと、$60÷2=30$本。
正二十面体の場合$3×20=60$本だけどダブりをなくすと、$60÷2=30$本。

土屋先生
次は頂点の数を考えてみよう。頂点と面についてどんな関係があるかな?考え方はさっきと同じで全体を出してからかぶっているところを探すだよ。

マサヤ君
たぶんわかった気がします!
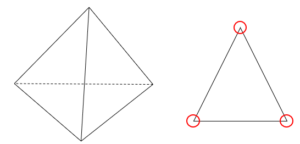
正四面体は正三角形が4個あるので、頂点の数は全部で$3×4=12$(頂点の数×面の数)個あるけど、1つの頂点は3個の面から成り立っているからダブリが出てくる。だから$12÷3=4$となるはず!

土屋先生
お見事!続けて他の頂点の数も出してみよう!

マサヤ君
はい。正六面体は正方形が6個あるので、頂点の数は全部で$4×6=24$(頂点の数×面の数)個あるけど、1つの頂点は3つの面から成り立っているからダブリが出てくる。だから$24÷3=8$
正八面体は正三角形が8個あるので、頂点の数は全部で$3×8=24$(頂点の数×面の数)個あるけど、1つの頂点は4つの面から成り立っているからダブリが出てくる。だから$24÷4=6$
正十二面体は正五角形が12個あるので、頂点の数は全部で$5×12=60$(頂点の数×面の数)個あるけど、1つの頂点は3つの面から成り立っているからダブリが出てくる。だから$60÷3=20$
正二十面体は正三角形が20個あるので、頂点の数は全部で$3×20=60$(頂点の数×面の数)個あるけど、1つの頂点は5つの面から成り立っているからダブリが出てくる。だから$60÷5=12$あっていますか?

土屋先生
完璧だね!では表にまとめてみるよ!
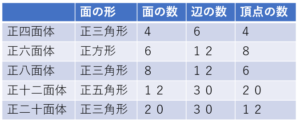
このようにわからなくても考えて導くことができるんだよ!そんなに難しくなかったでしょう。

スワンちゃん
ある多面体について以下の法則が成り立ちます。
$($頂点の数$)-($辺の数$)+($面の数$)=2$
これを「オイラーの多面体の法則」といいます。
1、頂点の数と辺の数がわかれば面の数が出せます。
(正四面体の場合、$4-6+($面の数$)=2$より面の数は$4$)
2、頂点の数と面の数がわかれば辺の数が出せます。
(正四面体の場合、$4-($辺の数$)+4=2$より辺の数は$6$)
3、面の数と辺の数がわかれば頂点の数が出せます。
(正四面体の場合、$($頂点の数$)-6+4=2$より辺の数は$4$)
他の多面体の形でも確かめてみてにゃ。

土屋先生
では問題です。図は何面体でしょうか。
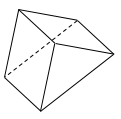

マサヤ君
面の数を数えればよいから、五面体です。
角柱・円柱と角錐・円錐
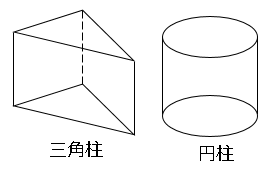
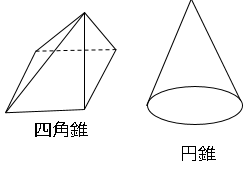
図のような図形をそれぞれ角柱・円柱と角錐・円錐という。

ユリコさん
先生違いがよくわからないのですが・・・?

土屋先生
では説明します。まずは柱とは錐とは?それぞれなんでしょうか?図を見てみてください。何か特徴はありませんか?



ユリコさん
柱の特徴は底面をそのまま上にどんどん乗せたような図の気がします。紫の図形は円を重ねてできた図で、オレンジの図形は星型を重ねてできた図形です。

土屋先生
その通りですね!柱の特徴は底面の図形を重ねたものになります。名前の付け方はどうなるでしょうか?

マサヤ君
三角柱は底面が三角形なのでそれに柱をつけて三角柱になっていると思います。緑の図形は底面が六角形なので六角柱、青の図形は底面が五角形なので五角柱だと思われます。つまり名前の法則は「底面の形+柱」をつけたものですね。だから紫の図形は底面が円なので円柱となるはず。

土屋先生
その通りだよ!まとめると柱とは底面を重ねた図形のことで、名前は「底面の形+柱」だね!では錐の特徴を考えてみよう。

錐の部分は「銀色の部分」だよ。柄の部分は円柱だね。

ユリコさん
彫刻刀で似たようなものを見ました!でも図を見てもパッとしませんが・・・なんか痛そうです(笑)


土屋先生
それも特徴の1つかな(笑)正しくは「ある1点」から底面に線が繋がっている図形のことを指します。赤い点(1点)から底面に赤線がつながっているね。
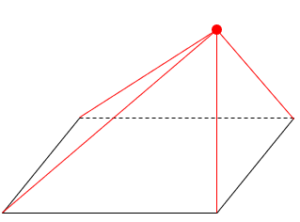
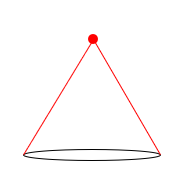
2点とかになると錐ではなくなるから注意が必要だよ。名前の付け方はわかるかな?

ユリコさん
たぶん同じ法則ですね。名前は「底面の形+錐」ですね。

土屋先生
そうですね!ちゃんと推測できていますね!

スワンちゃん
まとめだにゃん!
➀柱とは底面が重なったもので、名前のつけ方は「底面の形+柱」
➁錐とは「ある1点」から底面に線が繋がったもので、名前のつけ方は「底面の形+錐」
色々な展開図
立体を展開したときの図を展開図といいます。

マサヤ君
小学校でもやりましたね!

土屋先生
そうそう!展開図は小学生でも扱っているね。サイコロ(立方体)の展開図だね。

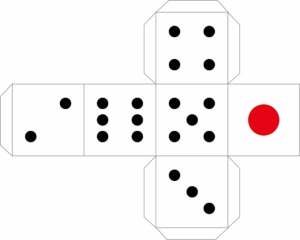
サイコロの目は足すと7になるって法則があったね。覚えている?今回は立方体以外の展開図を考えてみるよ。

マサヤ君
ってことは柱・錐の展開図も書くのですか?

土屋先生
もちろんだよ!でもそんな難しくないから平気だよ!
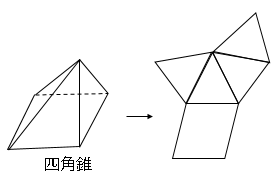
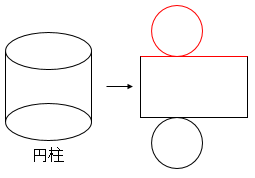
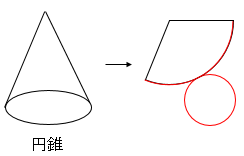
円柱・円錐の赤部分は同じ長さになります。つまり円柱の場合は円周=長方形の1辺になります。円錐の場合は円周=弧の長さになります。
注意:図の展開図は一例になるので、他にも色々な書き方があります。

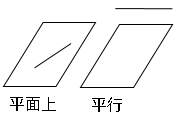
平行・交わる・ねじれの位置
平行とは2直線が交わらないこと。交わるとは2直線が交わること。ねじれの位置とは2直線が平行でもなく交わらないこと。
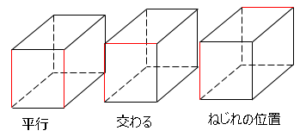
図は例となります。他にもあるので注意しましょう。

意味を理解したら問題を解いてみましょう。
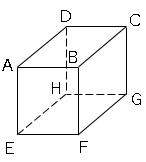
図の直方体について次の問いに答えなさい。答えは複数あります。
(1)辺$AB$と平行な辺はどれですか。
(2)辺$BF$とねじれの位置にある辺はどれですか。
(3)辺$BC$とねじれの位置にある辺はどれですか。
(4)辺$DH$と垂直に交わる辺はどれですか。
直線と平面の関係
基本的には上記の平行・交わる・ねじれの位置の関係と変わりません。


では問題を解いてみましょう。
図の直方体について次の問いに答えなさい。答えは複数あります。
(1)辺$AB$と垂直な面はどれですか。
(2)辺$AB$と平行な面はどれですか。
(3)面$BFGC$と垂直な辺はどれですか。
(4)面$ABCD$と平行な辺はどれですか。

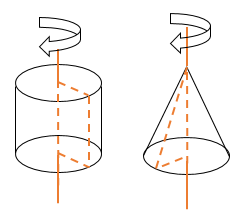
回転体
円柱や円錐のように、1つの直線を軸として平面図形を回転させてできる立体を回転体と呼ぶ。円柱は長方形を1回転させたもの。円錐は三角形を1回転させたもの。
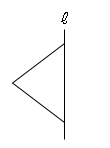
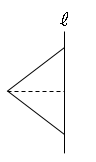
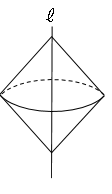
では問題を解いてみましょう。直線$ℓ$を軸としたときに、1回転させてできる立体を書きましょう。
立面図と平面図
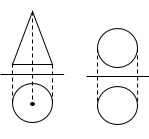
立体を真正面から見た図を立面図という。真上から見た図を平面図という。上記2つを合わせて投影図という。
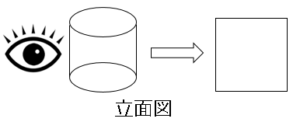
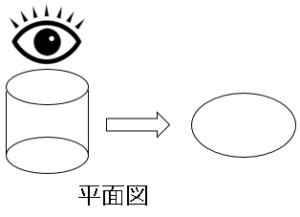
意味を理解したら問題を解いてみましょう。図の投影図で書かれた立体の名称は?








ディスカッション
コメント一覧
(人”▽`)ありがとう☆
どういたしまして!