オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
3980 Views
2018年3月19日図形の性質と証明中学２年生
問１
図のように、$AB=AC$,∠$BAC=90°$の直角二等辺三角形の頂点$A$を通る直線に、頂点$B$,$C$から垂線をひき、その交点をそれぞれ$P$,$Q$とする。このとき$BP+CQ=PQ$となることを証明しなさい。
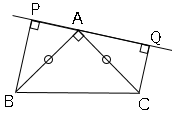
証明の問題は図に書いて理解した状態で書くと楽です。
長さの足し算を証明する場合は
三角形を証明してからやるとうまくいきます。（経験から）
わからない場合は
角や辺を文字で置くと考えやすくなります。
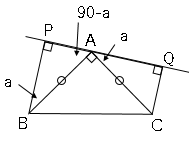
△$APB$と△$CQA$において、
垂線より∠$APB=$∠$CQA$ ・・・①
△$ABC$は直角二等辺三角形より$AB=CA$・・・②
∠$PAB=180-$∠$APB-$∠$PBA=180-90-$∠$PBA=90-$∠$PBA$
∠$CAQ=180-$∠$CAB-$∠$PAB=180-90-$∠$PAB=90-$∠$PAB=90-(90-$∠$PBA)=$∠$PBA$
よって
∠$CAQ=$∠$PBA$・・・➀、②、③より
斜辺と１つの鋭角がそれぞれ等しいから、△$APB≡$△$CQA$
合同な図形の対応する辺は等しいから、$BP+CQ$$=QA+AP$$=PQ$
よって$BP+CQ=PQ$
問２
図のように、線分$AB$上に点$C$をとり、$AC$,$CB$を、それぞれ１辺とする正三角形△$ACD$と△$CBE$を$AB$の同じ側に作る。また、$AE$と$BD$の交点を$F$､$CE$と$BD$の交点を$G$とする。△$ACE≡$△$DCB$を証明しなさい。
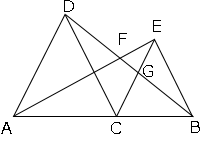
△$ACE≡$△$DCB$に関して、わかる角度・辺を図に書いてみましょう。
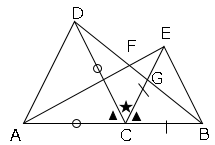
△$ACE$と△$DCB$において
正三角形$ACD$より$AC=DC$・・・①
正三角形$CBE$より$CE=CB$･･･②
∠$ACE=$∠$ACD+$∠$DCE=60+$∠$DCE$
∠$DCB=$∠$ECB+$∠$DCE=60+$∠$DCE$
よって∠$ACE=$∠$DCB$・・・③
➀、②、③より
２辺とその間の角がそれぞれ等しいので
△$ACE≡$△$DCB$
問３
図において、四角形$ABCD$は正方形である。$E$は、辺$BC$上にあって$B$,$C$と異なる点である。$A$と$E$を結ぶ。$F$は、$B$から線分$AE$に引いた垂線と線分$AE$との交点である。$G$は、$D$から線分$AE$に引いた垂線と線分$AE$との交点である。△$ABF≡$△$DAG$を証明せよ。
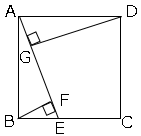
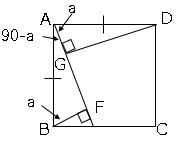
△$ABF$と△$DAG$において
仮定より$AB=AD$･･･①､∠$AFB=$∠$AGD$･･･②
また
∠$BAF=180-90-$∠$ABF=90-$∠$ABF$
∠$BAF=$∠$BAD-$∠$GAD=90-$∠$GAD$
よって
$90-$∠$ABF=90-$∠$GAD$
∠$ABF=$∠$GAD$･･･③
➀、②、③より
斜辺と１つの鋭角がそれぞれ等しいので、
△$ABF≡$△$DAG$
問４
図のように平行四辺形$ABCD$の辺$CD$の中点を$M$とし、$AM$の延長と辺$BC$の延長との交点を$E$とする。$BC=EC$を証明しましょう。
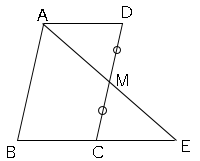
平行四辺形だから$AD=BC$ゆえに$AD=EC$を示せればよい。
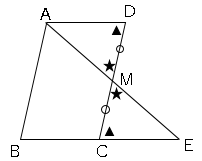
△$ADM$と△$ECM$において、
仮定より、$DM=CM$・・・➀
対頂角より、∠$AMD=$∠$EMC$・・・➁
$AD$//$BE$より、錯角が等しいので∠$ADM=$∠$ECM$・・・➂
➀、➁、➂より
１辺その両端の角がそれぞれ等しいので、
△$ADM≡$△$ECM$
対応する辺はそれぞれ等しいので、
$AD=EC$
平行四辺形より対応する辺の長さは等しいので、
$AD=BC$
よって
$BC=EC$
不明点があればコメントよりどうぞ。