最短距離と関数の問題

問題２０

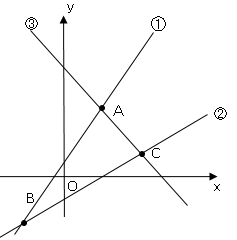
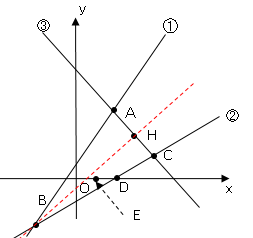
図で直線①、②、③はそれぞれ、$y=2x+1,y=\displaystyle \frac{x}{2}-2$,$y=ax+b(a<0)$である。
点$A$は直線①、③の交点で$A$の座標は$(3,7)$である。
点$B$は直線①、②の交点である。点$C$は直線②、③の交点である。
(1)直線②と$x$軸の交点を$D$とし、線分$OD$の中点を$E$とする。
$y$軸上に点$F$を$AF+FE$の長さが最も短くなるようにとるとき、点$F$の$y$座標を求めよ。
(2)$x$軸上の$x<0$に対応する部分に点$G$を、△$ABC$の面積と△$GBC$の面積が等しくなるようにとるとき、点$G$の$x$座標を求めなさい。
(3)点$B$から直線③に垂線を引き、直線③との交点を$H$とする。
$AH=CH$となるとき、点$C$の$x$座標を$t$とし、方程式を作って点$C$の座標を求めよ。

(1)


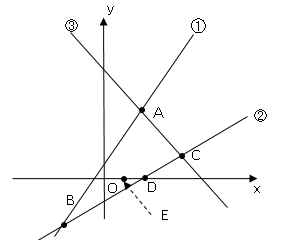
直線②と$x$軸との交点$D$は$(4,0)$、点$E$は線分$OD$の中点なので点$E(2,0)$となる。



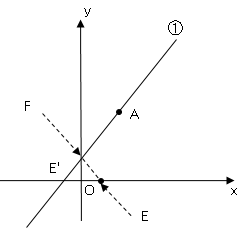
$AF+FE$の長さが最小になるとは、点$E$を$y$軸に対して対象移動した点$E’$が直線$AF$上にあることである。
よって直線$AF$の式を求める。$1$次関数$y=ax+b$に点$A,E’$の値を代入
$\begin{equation}\begin{cases}\; 7=3a+b･･･① \\\; 0=-2a+b･･･②\end{cases}\end{equation}$
これより$b=\displaystyle \frac{14}{5}$ゆえに点$F$の$y$座標は$\displaystyle \frac{14}{5}$

(2)


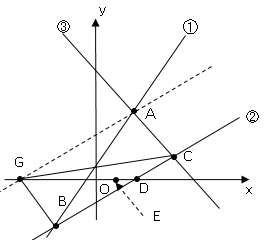
△$ABC$と△$GBC$の面積が等しいので、$BC$を底辺とすると高さは共通になる。
よって直線$BC$と$AG$の傾きは等しく$y=\displaystyle \frac{x}{2}+b$これが点$A$を通るので、
$7=\displaystyle \frac{3}{2}+b$
$b=\displaystyle \frac{11}{2}$
これより直線$AG$は$y=\displaystyle \frac{x}{2}+\displaystyle \frac{11}{2}x$軸上なので、点$G$の$y$座標は$0$
よって
$0=\displaystyle \frac{x}{2}+\displaystyle \frac{11}{2}$
$x=-11$
$G$の$x$座標は$-11$

(3)



$AH=CH$なので、△$BAC$は二等辺三角形になる。
よって
$BC=BA$
$BC²＝(-2-t)²+(-3-(\displaystyle \frac{t}{2}-2))²$
$BC＝\sqrt{\displaystyle \frac{5t²}{4}+5t+5}$

また
$BA²=(-2-3)²+(-3-7)²$
$BA=\sqrt{125}$

ゆえに
$BC=BA$
$\sqrt{\displaystyle \frac{5t²}{4}+5t+5}=\sqrt{125}$
$\displaystyle \frac{5t²}{4}+5t+5=125$
$\displaystyle \frac{t²}{4}+t+1=25$
$t²+4t+4=100$
$(t+2)²=100$
$(t+2)=±10$
$t=-2±10$
$t=8,-12$
$t=8$のとき、点$C$の座標は$(8,2)$
$t=-12$のとき、点$C$の座標は$(-12,-8)$これは$a<0$に反する。
よって$C$の座標は$(8,2)$