最短距離と三平方の定理
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
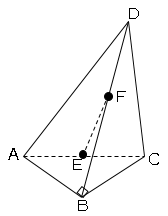
図$1$は$AB=BC=6cm,∠ABC=90°$の直角二等辺三角形$ABC$を底面とし、$BD=12cm$を高さとする三角錐である。また、2点$E,F$はそれぞれ辺$AC,BD$の中点である。
1、この三角錐の体積を求めなさい。
2、$2$点$E,F$間の距離を求めなさい。
3、三角錐に側面上に、図$2$のように点$A$から辺$CD$上の点まで、長さが最も短くなるように引いた線の長さを求めなさい。

土屋先生
1はそんなに難しくないからサクッとやっちゃうね!
底面が△$ABC$で高さが$BD$の三角錐なので、
$6×6÷2×12÷3$
$=72$
三角錐の体積$=$底面積$×$高さ$(12)÷3$を使ったよ。この場合の底面積は直角二等辺三角形$ABC$だから、求める面積は三角形と同じだね。底面積$=$底辺$(6)×$高さ$(6)÷2$を使ったよ
みんな大丈夫?

マサヤ君

ユリコさん


土屋先生

マサヤ君
とりあえず色々な辺の長さを出してます。$BF$の長さは$BD$の長さの半分なので$6$ですね。・・・こんな感じでいいんですかね?

土屋先生
悪くないよ!長さを求める場合は相似、合同、三平方の定理を使う場合が多いけどどれも辺の長さを必要とするから、色々な線の長さを出しておいた方がいいね。あとは角に注目することだね。わかるかな?

ユリコさん
先生!わかった!(1)で高さを出していることから、△$EBF$の$∠EBF=90°$ですよね。三平方の定理を使える気がしますね!

土屋先生
いいね!その三角形に注目してみよう。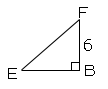
すると$BE$の長さがわかれば、$EF$の長さも三平方の定理$(EF²=BE²+BF²・・・☆)$からわかるね。そしたら$BE$の長さを出してみよう!どの三角形に注目するかな?ちなみに三平方の定理?って何それって人はここから復習しようね!そんなに難しくないよ!

マサヤ君
次は僕の番だね(笑)先生△$ABC$だと思います。理由は$AC$の中点が$E$と書いてあるから怪しいですね!
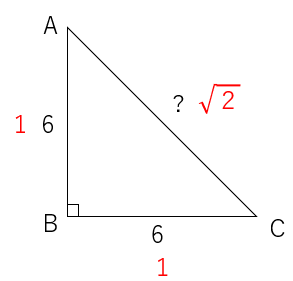
でもって$AE$の長さは$AC$の長さの半分だからまずは$AC$の長さを出します。
△$ABC$は直角二等辺三角形で角度が$45,45,90$なので、辺の比がそれぞれ$AB:BC:AC=1:1:\sqrt{2}$なので
$AC=6\sqrt{2}$です。
$(AB:AC=1:\sqrt{2}$
$6:AC=1:\sqrt{2}$
$AC=6\sqrt{2})$
(辺の比は$a:b=c:d$の場合$ad=bc$となったね!外$(a)$と外$(d)$をかけて内$(b)$と内$(c)$をかける。)
だから$AE=3\sqrt{2}$です。

土屋先生
いったんまとめよう。このような図になっているね。マサヤ君続けて。
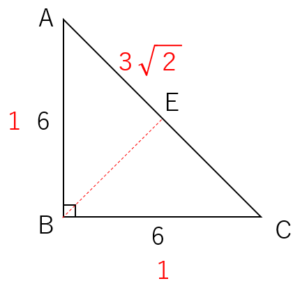

マサヤ君
はい。そして$BE$の長さは△$ABE$に三平方の定理を用いて
$BE²=AB²-AE²$
$BE²=6²-(3\sqrt{2})²$
$BE²=18$
$BE=3\sqrt{2}$
になります。
$☆$より$EF²=BE²+BF²$なので、
$EF²=(3\sqrt{2})²+6²$
$EF²=18+36$
$EF²=54$
$FE=3\sqrt{6}$です。

土屋先生
意外に長い説明になったけど、やっていることは三平方の定理を使って計算をするだけだね。次は3の問題にチャレンジしてみよう!

マサヤ君
ん~正直よくわからないですね・・・線が最短とはどういう状況なのだろうか?

土屋先生
こう考えてみよう。展開図を書いて点$A$から垂線を引けば、最短距離になりそうだよ。わからないって?具体的に考えてみよう。

点Aから線分に最短距離を引く場合はどのように考えるだろうね。少しでも上にずれたり下にずれたりすると、その分だけ長さが長くなって最短距離にならなくなってしまうね。その場合は垂線を引けば上にも下にもずれないね。

マサヤ君
なるほど!だから垂線を引けばいいってことですね!
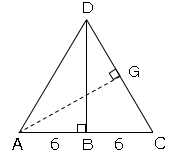
点$G$を$DC$との交点とすると、$AG$の長さを求めればいいんですね。

土屋先生
ではどのようにしたら$AG$の長さが求まるだろうね?わかるかな?結構よく使う方法なんだよ。

ユリコさん
色んな線の長さを出してみたらいいと思います。$DB$の長さは$12$なので、三平方の定理より$DA$の長さは求まります。
$DA²=DB²+BA²$
$DA²=12²+6²$
$DA²=144+36$
$DA²=180$
$DA=6\sqrt{5}$
でもその先が・・・。

土屋先生
これはよく使う方法だから覚えておいてね。

直角三角形$DAG$と$CAG$が図のように$AG$を共通しているとき、直角三角形$DAG$に三平方の定理を用いて、$AG²=AD²-DG²$となり、直角三角形$CAG$に三平方の定理を用いて、$AG²=AC²-GC²$となる。
つまり$AD²-DG²=AC²-GC²(★)$になるんだよ。
さっき$AD$は求めてあるね。更に△$DAB$と△$DCB$は合同だから$DA=DC$になるよ。

証明の補足だニャン。
△$DAB$と△$DCB$において
$AB=CB=6$・・・➀
$∠DAB=∠DCB=90°$・・・➁
$DB$は共通・・・➂
➀、➁、➂より
2辺とその間の角がそれぞれ等しいので、
△$DAB≡$△$DCB$
対応する辺の長さは等しいので、
$DA=DC$

土屋先生
スワンちゃん補足ありがとう。不安な人は「三角形の合同と証明」の復習はここからできるよ。

土屋先生
最後に$GC=x$とおくと、$DG=6\sqrt{5}-x$となるのであとは$★$にそれぞれ代入して計算すればいいね。
$AD²-DG²=AC²-GC²$
$(6\sqrt{5})²-(6\sqrt{5}-x)²=12²-x²$
$180-(180-12\sqrt{5}x+x²)=144-x²$
$12\sqrt{5}x-x²=144-x²$
$12\sqrt{5}x=144$
$\sqrt{5}x=12$
$x=\displaystyle \frac{12}{\sqrt{5}}$
これを$AG²=AC²-GC²$に代入して
$AG²=12²-(\displaystyle \frac{12}{\sqrt{5}})²$
$AG²=12²-\displaystyle \frac{12²}{5}$$(12²=144$だけど後で計算するから$12²$の方がいいね$)$
$AG²=12²(1-\displaystyle \frac{1}{5})$
$AG²=12²(\displaystyle \frac{5-1}{5})$
$AG²=12²(\displaystyle \frac{4}{5})$
$AG²=24²(\displaystyle \frac{1}{5})$
$AG=24(\displaystyle \frac{1}{\sqrt{5}})$
$AG=\displaystyle \frac{24\sqrt{5}}{5}$
ついてこれた?大丈夫?
1、
底面が△$ABC$で高さが$BD$の三角錐なので、求める体積は
$6×6÷2×12÷3$
$=72$
2、以下の図のように考える。
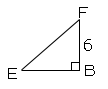
本文より$BD$が三角錐の高さなので∠$FBE=90°$になる。
またBEの長さは、以下の図より求めることができる。
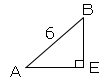
$AE$の長さは$AC$の長さの半分で、△$ABC$は角度が$45,45,90$なので、
$AC=6\sqrt{2}$よって$AE=3\sqrt{2}$
これより$BE$の長さは
$BE²=AB²-AE²$
$BE²=6²-(3\sqrt{2})²$
$BE=3\sqrt{2}$
最後に$EF$の長さは
$EF²=BE²+BF²$
$EF²=(3\sqrt{2})²+6²$
$EF²=54$
$EF=3\sqrt{6}$
3、
以下の図のように点$G$をとると求める答えは$AG$の長さとなる。

(最短距離とは点Aからの垂線である。)
$AD$の長さは、△$DAB$において三平方の定理より
$AD²=AB²+DB²$
$AD²=6²+12²$
$AD²=180$
$AD=6\sqrt{5}$
$DC$は△$ADB≡$△$CDB$より
$AD=DC=6\sqrt{5}$
ここで$CG=x$とおくと、
$DG=6\sqrt{5}-x$となる。
△$AGC$に三平方の定理を用いて、
$AG²=AC²-CG²$
$AG²=12²-x²$・・・①
△$AGD$に三平方の定理を用いて、
$AG²=AD²-DG²$
$AG²=(6\sqrt{5})²-(6\sqrt{5}-x)²$・・・②
➀=➁より
$12²-x²=(6\sqrt{5})²-(6\sqrt{5}-x)²$
$144=12\sqrt{5}x$
$x=\displaystyle \frac{12}{\sqrt{5}}$
これを➀に代入して
$AG²=12²-(\displaystyle \frac{12}{\sqrt{5}})²$
$AG²=12²(1-\displaystyle \frac{1}{5})$
$AG²=12²(1-\displaystyle \frac{4}{5})$
$AG=\displaystyle \frac{24\sqrt{5}}{5}$
求める最短の長さは$\displaystyle \frac{24\sqrt{5}}{5}$

土屋先生
今日のまとめ
➀色々な辺の長さ・角の大きさを出すと相似・合同・三平方の定理が使える。
➁同じ辺を三平方の定理で求めて、イコールで結ぶ。

土屋先生
不明点があればLINEもしくは下記コメント欄よりお願いします。





ディスカッション
コメント一覧
まだ、コメントがありません