【面積】平行四辺形の面積の変わった求め方の問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
8432 Views
問題１８図のような平行四辺形の面積を求めよ。
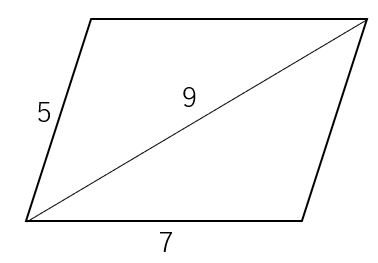
方針
平行四辺形の面積は底辺×高さであり、その高さを求める。
高さを出すために補助線を引いて求める。
高さを出すために補助線を引いて求める。
補助線を引く
以下の図のように点を置き補助線を引く。
点$BE$の長さを$x$とおく。
（※$DE$の長さを$x$としてもいいが、計算が複雑になる。）
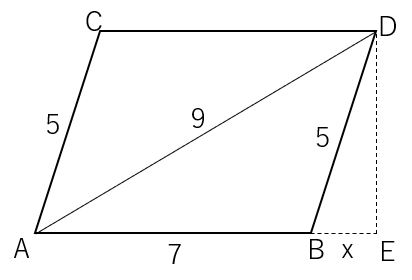
すると、△$DEB$に三平方の定理を用いて、
$DE²＝DB²-BE²$
$DE²＝5²-x²$
$DE＝\sqrt{25-x²}$
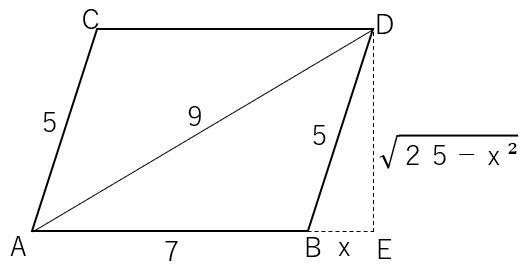
更に△$ADE$に三平方の定理を用いて、
$AD²＝AE²+DE²$
$9²＝(7+x)²+(\sqrt{25-x²})²$
$81＝49+14x+x²+25-x²$
$-14x＝-7$
$x＝\displaystyle \frac{1}{2}$
これより、
$DE＝\sqrt{25-(\displaystyle \frac{1}{2})²}$
$DE＝\sqrt{25-(\displaystyle \frac{1}{4})}$
$DE＝\displaystyle \frac {3\sqrt{11}}{2}$
よって平行四辺形の面積は、
$7×\displaystyle \frac {3\sqrt{11}}{2}$
$=\displaystyle \frac {21\sqrt{11}}{2}$
不明点があればコメント欄よりお願いします。