体積を2通りで出す問題
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
6428 Views
問題18直方体$ABCD-EFGH$で、線分$DM$の長さを$2cm$とするとき、
(1)△$FAM$の面積を求めなさい。
(2)点$B$と面$FAM$の距離を求めなさい。
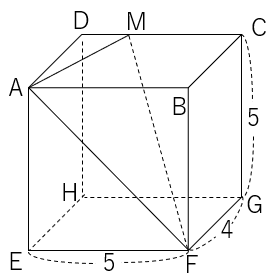
(1)△$FAM$の面積を求めなさい。
(2)点$B$と面$FAM$の距離を求めなさい。

方針
(1)と(2)の関係を考える。
面積を求める。
(1)
三角形のそれぞれの辺の長さを求めると、
三平方の定理より、
$AM²=AD²+DM²$
$AM²=4²+2²$
$AM=2\sqrt{5}$
また三平方の定理より、
$AF²=AE²+EF²$
$AF=5\sqrt{2}$
さらに三平方の定理より、
$MF²=MC²+CG²+GF²$
$MF=5\sqrt{2}$
底辺を$AM$とみたときの高さ$h$は
$h²=AF²-(\displaystyle \frac{2\sqrt{5}}{2})²$
$h=3\sqrt{5}$
求める面積は
$2\sqrt{5}×3\sqrt{5}÷2$
$=15$
体積を2通りで求める。
(2)
点$B$と面$FAM$の距離とは、
三角錐$B-FAM$の底面を$FAM$とした場合の高さ($h$)となる。
直接求めることができないので、体積を2通りで表す。
1つ目、
△$AFM×h×\displaystyle \frac{1}{3}$
$=5h$
2つ目、
底面を△$ABF$とおくと三角錐$B-FAM$の体積は
$5×5÷2×4×\displaystyle \frac{1}{3}$
$=\displaystyle \frac{50}{3}$
1つ目と2つ目は同じ体積なので、
$5h=\displaystyle \frac{50}{3}$
$h=\displaystyle \frac{10}{3}$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません