三平方の定理
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
4288 Views
三平方の定理直角三角形の直角をはさむ$2$辺の長さを$a,b$、斜辺を$c$とすると次の関係が成り立つ。
$a²+b²=c²$
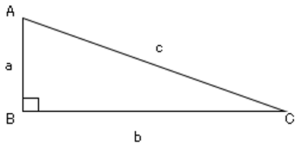
※斜辺とは$90$度の向かいの辺のことです。
$a²+b²=c²$
※斜辺とは$90$度の向かいの辺のことです。
では問題です。図で、$x$の値を求めましょう。
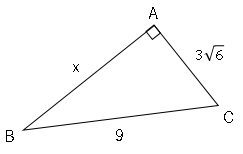
特別な直角三角形以下の２つの三角形は覚えておきましょう。
１.直角二等辺三角形の$3$辺の比は$1:1:\sqrt{2}$
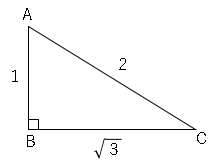
２.$3$つの角が$30°$,$60°$,$90°$の直角三角形の$3$辺の比は$1:2:\sqrt{3}$
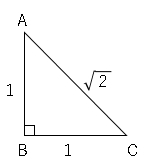
１.直角二等辺三角形の$3$辺の比は$1:1:\sqrt{2}$
２.$3$つの角が$30°$,$60°$,$90°$の直角三角形の$3$辺の比は$1:2:\sqrt{3}$
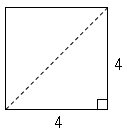
では問題です。図の正方形の対角線の長さを求めましょう。
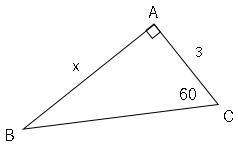
さらに問題です。図で、$x$の値を求めましょう。
円との関係円の中心から弦に引いた垂線はその弦を$2$等分する。
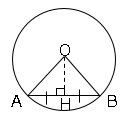
証明
$HB²=OB²-OH²$（三平方の定理より）
$HA²=OA²-OH²$（三平方の定理より）
円の半径なので
$OB=OA$
よって
$HB²=HA²$
$HB=HA$
証明
$HB²=OB²-OH²$（三平方の定理より）
$HA²=OA²-OH²$（三平方の定理より）
円の半径なので
$OB=OA$
よって
$HB²=HA²$
$HB=HA$
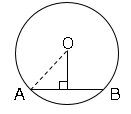
では問題です。半径$3cm$の円$O$で、弦$AB$の長さが$2\sqrt{5}cm$のとき、中心$O$から弦$AB$までの距離を求めましょう。
グラフとの関係座標平面上の$2$点$A(a,a’)$、$B(b,b’)$の間の距離$AB$は
$AB=\sqrt{(b-a)²+(b’-a’)²}$
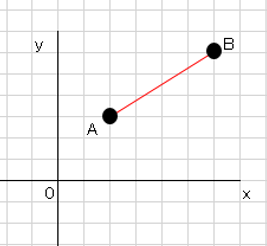
証明
$A(a,a’)$、$B(b,b’)$
図のように垂線を引くと、
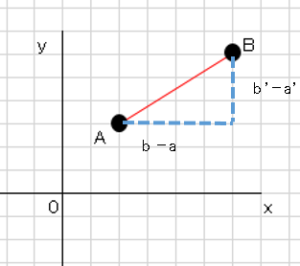
三平方の定理より
$AB²=(b-a)²+(b’-a’)²$
$AB=±\sqrt{(b-a)²+(b’-a’)²}$
$AB＞0$なので
$AB=\sqrt{(b-a)²+(b’-a’)²}$
これは図を書けばわかることなので、覚えなくてよいです。
$AB=\sqrt{(b-a)²+(b’-a’)²}$
証明
$A(a,a’)$、$B(b,b’)$
図のように垂線を引くと、
三平方の定理より
$AB²=(b-a)²+(b’-a’)²$
$AB=±\sqrt{(b-a)²+(b’-a’)²}$
$AB＞0$なので
$AB=\sqrt{(b-a)²+(b’-a’)²}$
これは図を書けばわかることなので、覚えなくてよいです。
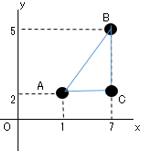
では問題です。$2$点間の距離を求めましょう。$B(7,5)$､$A(1,2)$
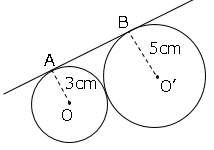
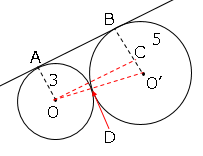
さらに問題です。図で、点$A,B$はそれぞれ円$O,O’$に共通な接線$ℓ$と円$O,O’$との接点である。線分$AB$の長さを求めましょう。
実際の受験問題を解いてみましょう。
受験問題
不明点があればコメント欄よりお願いします。