空間図形への応用
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
13962 Views
対角線の長さ1.縦、横、高さが$a,b,c$である直方体の対角線の長さは$\sqrt{a²+b²+c²}$
2.$1$辺が$a$である立体の対角線は$\sqrt{3a}$
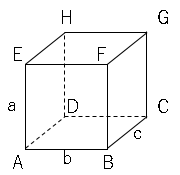
1の証明
縦、横、高さが$a,b,c$である直方体の対角線$(EC)$の長さを求めましょう。
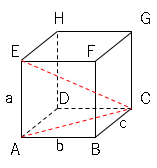
三角形$ABC$は$B$を直角とする直角三角形
なので$AC$の長さは三平方の定理より
$AC²=b²+c²$
また、三角形$ACE$は$A$を直角とする
直角三角形なので$EC$の長さは
三平方の定理より
$EC²=EA²+AC²$
$EC²=a²+b²+c²$
$EC=\sqrt{a²+b²+c²}$
これは線を引いてしまえばわかることなので、覚える必要はないです。
2.$1$辺が$a$である立体の対角線は$\sqrt{3a}$

1の証明
縦、横、高さが$a,b,c$である直方体の対角線$(EC)$の長さを求めましょう。

三角形$ABC$は$B$を直角とする直角三角形
なので$AC$の長さは三平方の定理より
$AC²=b²+c²$
また、三角形$ACE$は$A$を直角とする
直角三角形なので$EC$の長さは
三平方の定理より
$EC²=EA²+AC²$
$EC²=a²+b²+c²$
$EC=\sqrt{a²+b²+c²}$
これは線を引いてしまえばわかることなので、覚える必要はないです。
では問題です。図のような立体の対角線の長さを求めましょう。
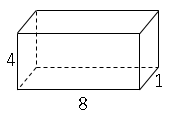
さらに問題です。
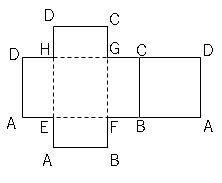
図は直方体に、頂点$A$から辺$EF$、$HG$を通って、$C$まで長さが最短になるようにひもをかけていたところをしめしている。
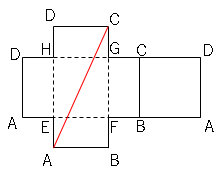
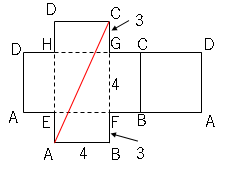
(1)展開図に、長さが最短になるようにかけたひものようすを書き入れましょう。
(2)長さが最短になるようにかけたときのひもの長さを求めましょう。
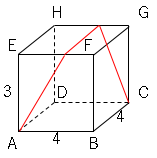
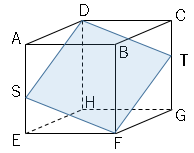
さらに問題です。$1$辺$8cm$の立方体の頂点や返上の点を結んでできる次の図形(影の部分)の面積を求めなさい。
ただし、点$S$は$AE$の中点・点$T$は$CG$の中点とする。
実際の受験問題を解いてみましょう。
受験問題
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません