体積の工夫した求め方

問題１０

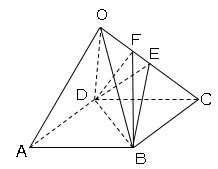
図の立体Ｏ-ＡＢＣＤは、正方形ＡＢＣＤを底面とする正四角すいである。Ｅは辺ＯＣ上の中点、Ｆは辺ＯＣ上の点で、ＯＦ：ＦＣ＝１：２である。正四角すいＯ-ＡＢＣＤのすべての辺の長さを６ｃｍとする。
（１）線分ＢＦの長さはいくつになるか。
（２）Ｂ,Ｄ,Ｅ,Ｆを頂点とする三角すいの体積を求めよ。

方針

ＢＦが入っている△ＯＢＣを取り出して考える。

どこを底面、高さにしたら（１）を利用できるか考える。

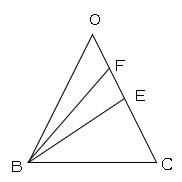
正三角形なので、ＢＣ＝６、点Ｅは辺ＯＣの中点なので、ＥＣ＝３。
また∠ＣＢＥは正三角形の半分なので、３０°
これより△ＢＥＣは３０、６０、９０°の特別な三角形となる。

よって
$BE:EC=\sqrt{3}:1$
$BE:3=\sqrt{3}:1$
$BE=3\sqrt{3}$

またＯＦの長さは２より、ＦＥの長さは３－２＝１となる。
△ＦＥＢは∠ＦＥＢ＝９０°の直角三角形なので、３平方の定理よりＦＢの長さは
$FB²=FE²+EB²$
$FB²=1²+(3\sqrt{3})²$
$FB=2\sqrt{7}$

この場合は底面を△ＥＤＢ、高さをＦＥとする。
底面積を求める。

ＤＢの長さは正方形の対角線より
$DB=6\sqrt{2}$
点Ｅから垂線を降ろし交点をＧとすると、

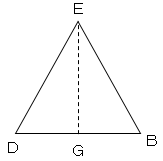
△ＥＤＧと△ＥＢＧは合同となる。
（ＤＥ＝ＢＥ、∠ＥＧＤ＝∠ＥＧＢ＝９０、ＥＧは共通）

なのでＤＧはＤＢの半分となり、
$DG=3\sqrt{2}$
△ＥＤＧについて、３平方の定理よりＥＧの長さは
$EG²=ED²-DG²$
$EG²=(3\sqrt{3})²-(3\sqrt{2})²$
$EG=3$

これより底面積は
$DB×EG÷2$
$=6\sqrt{2}×3÷2$
$=9\sqrt{2}$

よって求める体積は
$9\sqrt{2}×1÷3$
$=3\sqrt{2}$