オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
3867 Views
2019年3月16日三平方の定理中学3年生
問1図のように、関数$y=\displaystyle \frac{1}{3}x²$のグラフと直線が$2$点$A,B$で交わっている。
次の問いに答えましょう。
(1)線分$AB$の長さを求めましょう。
(2)△$OAB$の面積を求めましょう。
(3)点$O$と直線$AB$の距離を求めましょう。
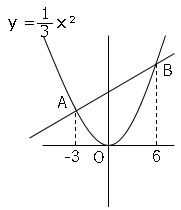
(1)
点$A$は$(-3,3)$、点$B$は$(6,12)$
これと三平方の定理より
$AB²=9²+9²$
$AB²=2×81$
$AB=9\sqrt{2}$
(2)
直線$AB$を求めると
$\begin{eqnarray} \left\{ \begin{array}{l} 3=-3a+b \\ 12=6a+b \end{array} \right.\end{eqnarray}$
この連立方程式をといて
$y=x+6$
△$OAB$
$=6×3÷2+6×6÷2$
$=27$
△$OAB$の面積は
$27$
(3)点$O$からの垂線と直線$AB$との交点を$C$とする。
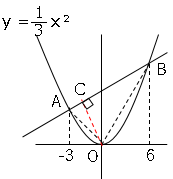
三角形の面積より
$27=AB×CO÷2$
$27=9\sqrt{2}×CO÷2$
$CO=\displaystyle \frac{27×2}{9\sqrt{2}}$
$CO=\displaystyle \frac{27×2×\sqrt{2}}{9×2}$
$CO=3\sqrt{2}$
問2図で、$1$辺が$11cm$の正三角形$ABC$がある。
$BD=5cm$、$DE⊥AC$、$DF//CA$となるように、辺$BC$上に点$D$、辺$AC$上に点$E$、辺$AB$上に点$F$をとる。
このとき線分$EF$の長さを求めましょう。
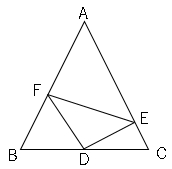
ポイントは「正三角形だから角が$60°$なので、特別な三角形がある」
$DF//AC$より
$∠FAE=∠BFD=60°$
△$BFD$は正三角形になり、
これより$FD=5cm$
△$ECD$について
これは$30、60、90°$の三角形より
$2:√3=6:ED$
$ED=3√3$
また∠$FDE=180-$∠$FDB-$∠$EDC$
$=180-60-30$
$=90$
三平方の定理より
$FE²=5²+(3\sqrt{3})²$
$FE²=52$
$FE=2\sqrt{13}$
問3 図で、長方形$ABCD$を頂点$C$が辺$AD$の中点$M$と重なるように折り、$DF=x$とするとき、次の問いに答えましょう。
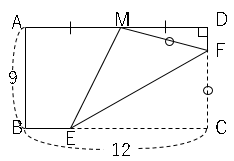
(1)$MF$の長さを$x$の$1$次式で表しましょう
(2)直角三角形$DFM$に着目して、方程式を作りましょう。
(3)$DF$の長さを求めましょう。
(1)
$MF=FC$なので
$MF=9-x$
(2)
三平方の定理より
$(9-x)²=x²+6²$
(3)
$81-18x+x²=x²+36$
$-18x=-45$
$x=\displaystyle \frac{5}{2}$
$DF$の長さは$\displaystyle \frac{5}{2}cm$
問4図で、辺の長さがすべて$12cm$の正四面錐で、$M$,$N$はそれぞれ辺$OC$、$OD$の中点である。次の問いに答えましょう
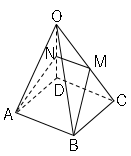
(1)線分$NM,NA,MB$の長さを求めましょう。
(2)台形$ABMN$の面積を求めましょう。
(1)
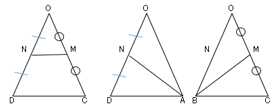
中点連結定理より
$MN=\displaystyle \frac{1}{2}×DC=6$
△$ONA$について
これは$30、60、90°$の三角形より
$6:NA=1:\sqrt{3}$
$NA=6\sqrt{3}$
同様に
$MB=6\sqrt{3}$
(2)
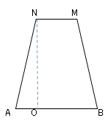
$AO$の長さは$(AB-NM)÷2$
$AO=(12-6)÷2$
$AO=3$
これより三平方の定理より
$(6\sqrt{3})²=3²+NO²$
$NO²=99$
$NO=3\sqrt{11}$
よって台形の面積は
$(6+12)× 3\sqrt{11}÷2$
$=27\sqrt{11}$
問5図は、$1$辺の長さが$6cm$の正四面体で、点$E$は辺$AB$の中点である。
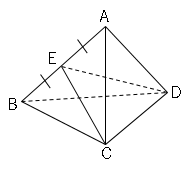
(1)線分$EC$の長さを求めましょう。
(2)△$ECD$の面積を求めましょう。
(3)正四面体の体積を求めましょう。
(1)
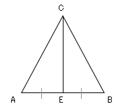
三角形$ABC$は正三角形なので
∠$A$は$60°$また、$E$は中点なので垂線となり∠$E$は$90°$
これより三角形$CAE$について
$30、60、90°$の三角形より
$3:EC=1:\sqrt{3}$
$EC=3\sqrt{3}$
(2)
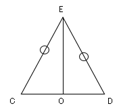
二等辺三角形の頂点から降ろした垂線と底辺の交わる点を$O$とする。
これは底辺の中点であるから
$CO=3、EC=3\sqrt{3}$
三平方の定理より
$EO²=(3\sqrt{3})²-3²$
$EO²=18$
$EO=3\sqrt{2}$
これより△$ECD$の面積は
$6×3\sqrt{2}÷2$
$=9\sqrt{2}$
(3)
$EA⊥EC$、$ EA⊥ED$、より$AE$は面$ECD$に垂直である。
よって
$A-ECD$の体積は
$9\sqrt{2}×3×\displaystyle \frac{1}{3}=9\sqrt{2}$
また$B-ECD$の体積は$A-ECD$の体積と同じなので
正四面体の体積は
$18\sqrt{2}$
実際の受験問題を解いてみましょう。
受験問題
不明点があればコメント欄よりお願いします。






















ディスカッション
コメント一覧
まだ、コメントがありません