円錐の最短距離

LINE@始めました。友達追加をよろしくお願い申し上げます。

勉強のやり方の相談・問題の解説随時募集しています！お気軽にＬＩＮＥしてください。

786 Views

2017年11月1日2018年3月9日立体の表面積と体積中学３年生, 難易度★★

問題１３

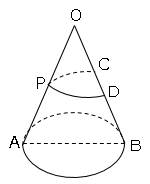
図に示した立体は、頂点がＯ、底面が長さ１５ｃｍの線分ＡＢを直径とする円、母線の長さが３０ｃｍの円すいである。
２点Ｃ，Ｄは母線ＯＢ上にあり、ＯＣ＝ＣＤ＝ＤＢである。点Ｐは母線ＯＡ上を動く点である。図のように点Ｃから点Ｐを経由して点Ｄまでひもをかける。
ひもの長さが最も短くなるように点Ｐをとるときのひもの長さは何ｃｍですか。

方針

（１）の問題の考え方

ひもの問題は展開図を書いて、ひもが直線になればよい。

（１）展開図をかく。

以下のような図を書く。（必要なとこだけ）

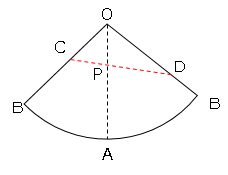
すると、線分ＣＤを求めればよいことがわかる。
ここでおうぎ形の角度に注目する。
（角度がわかれば三平方の定理が使えるから）

おうぎ形の弧の長さは中心角をａとすると、
$30×2×π×\displaystyle \frac{a}{360}$・・・➀
また、弧の長さは円周と同じなので
$15×π$・・・➁
➀＝➁より
ａ＝９０°

△ＯＣＤに三平方の定理を用いて、
$CD²=OC²+OD²$
$CD²=10²+20²$
$CD=10\sqrt{5}$