連立方程式と食塩水

問題６食塩水$A､B､C$がある。$A200g$と$B300g$を混ぜると､濃度$6.8%$の食塩水ができ､$B300g$と$C200g$を混ぜると､濃度$8.8%$の食塩水ができる。また､$A200g$と$C300g$を混ぜると$B$と同じ濃度になる。食塩水$A,B,C$のそれぞれの濃度を$x%,y%,z%$とするとき、方程式を用いて$x,y,z$を求めなさい。

（６）食塩の量は変わらないのでそれぞれ方程式を作る。

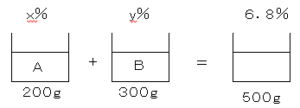
$200×\displaystyle \frac{x}{100}+300×\displaystyle \frac{y}{100}=500×\displaystyle \frac{6.8}{100}$
$2x+3y=34$･･･①


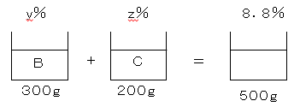
$300×\displaystyle \frac{y}{100}+200×\displaystyle \frac{z}{100}=500×\displaystyle \frac{8.8}{100}$
$3y+2z=44$･･･②


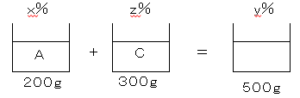
$200×\displaystyle \frac{x}{100}+300×\displaystyle \frac{z}{100}=500×\displaystyle \frac{y}{100}$
$2x+3z=5y$･･･③

$2x+3y=34$･･･①
$3y+2z=44$･･･②
$2x+3z=5y$･･･③

➀-③より
$8y-3z=34$･･･④

②×3+④×2より
$25y=200$
$y=8$
よって$z=10,x=5$食塩水$A,B,C$のそれぞれの濃度は$5$%,$8$%,$10$%