立体と最短距離

問題２図のように、正三角錐がある。ＡＢ＝ＡＣ＝ＡＤ＝９、ＢＣ＝ＣＤ＝ＢＤ＝６とする。正三角錐の辺ＡＢ上にＡＥ＝３となる点Ｅをとり、点Ｅを通り、面ＢＣＤに平行な面ＥＦＧより上の正三角錐を切り取り、立体を作る。

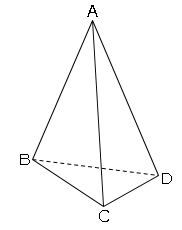
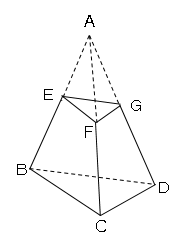
（１）△ＥＦＧの面積を求めよ。
（２）切り取った残りの立体の体積を求めよ。
（３）辺ＦＣ、ＧＤ上にそれぞれ点Ｋ，Ｌを、線分ＢＫ，ＫＬ，ＬＢの長さの和が最も小さくなるようにとるとき、ＢＫ＋ＫＬ＋ＬＢの長さを求めよ。

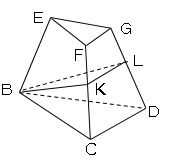
方針立体の問題は、部分的に取り出して考えるとわかりやすい。

➀面積を出すので、△ＥＦＧの辺の長さを求める。
➁△ＥＦＧ高さを求め、面積を出す。

➀Ａ－ＥＦＧの体積を求める。
➁Ａ－ＢＣＤの体積を求める。
➂➁－➀で残りの体積を出す。

➀展開して図を書く。
➁点Ａを中心とする円の上にＢ,Ｃ,Ｄがあるように考える。
➂相似な三角形を探す。

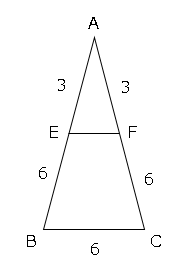
図より、△ＡＥＦ∽△ＡＢＣなので
$EF:BC=AE:AB$
$EF:6=3:9$
$EF=2$
同様に$FG=GE=2$となる。

次に点ＥからＦＧに垂線を引き、交点をＨとする。

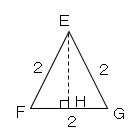
図よりＦＨ＝１、△ＥＦＨは３０、６０、９０°の特別な三角形より、
$EH=\sqrt{3}$
これより△ＥＦＧの面積は
$FG×EH÷2$
$=2×\sqrt{3}÷2$
$=\sqrt{3}$

（１）で面積は出ているので、高さを求める。
以下のように点Ａから補助線を引く。

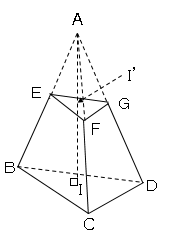
するとＡＩ’が高さになる。次にＥＩ’を求める。
※ＥＩ’が求まれば、三平方の定理よりＡＩ’が求まるので。
わかりにくいので、△ＥＦＧを取り出して考える。

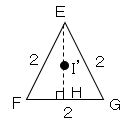
するとＩ’は∠ＥＦＧの二等分線となる。よって
$EI’:IH’=2:1$より
$EI’=\displaystyle \frac{2}{3}×EH$
$EI’=\displaystyle \frac{2\sqrt{3}}{3}$
よって△ＡＥＩ’で三平方の定理を用いて、
$AI’²=AE²-EI’²$
$AI’²=3²+(\displaystyle \frac{2\sqrt{3}}{3})²$
$AI’=\displaystyle \frac{\sqrt{69}}{3}$
よってＡ－ＥＦＧの体積は
$\sqrt{3}×\displaystyle \frac{\sqrt{69}}{3}÷3$
$=\displaystyle \frac{\sqrt{23}}{3}$

体積比は相似比の３乗より
Ａ－ＢＣＤの体積はＡ－ＥＦＧの体積の２７倍となる。
よって$\displaystyle \frac{27\sqrt{23}}{3}$

➁－➀より
$\displaystyle \frac{26\sqrt{23}}{3}$

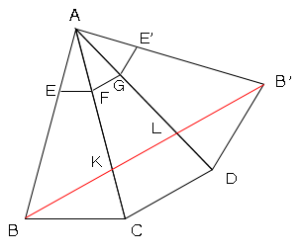
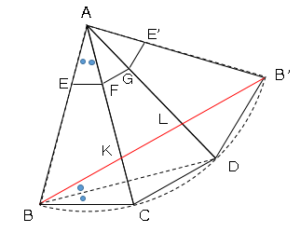
ＢＤに補助線を引くと、円周角の定理より図のような関係となる。
よって△ＢＡＣ∽△ＣＢＫ∽△ＫＡＬとなる。
これよりＢＣ＝ＢＫ＝ＢＬ＝６、また、
$BA:BC=CB:CK$
$9:6=6:CK$
$CK=4$
ゆえに$AH=5$
$AH:HI=BC:CH$
$5:HI=6:4$
$HI=\displaystyle \frac{10}{3}$
よって求める長さは
$6+\displaystyle \frac{10}{3}+6$
$=\displaystyle \frac{46}{3}$