正六角形と体積

問題３図１は底面ＡＢＣＤＥＦが１辺の長さが４ｃｍである正六角形で、側面がすべて合同な長方形の六角柱ＡＢＣＤＥＦＧＨＩＪＫＬを表しており、ＡＧ＝６ｃｍである。

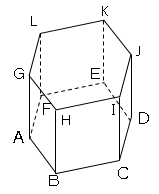
図２は、図１に示す立体において、点Ｇと点Ｉ、点Ｈと点Ｊ、点Ｈと点Ｌをそれぞれ結び、線分ＧＩと線分ＨＪ、ＨＬとの交点をそれぞれＰ，Ｑとしたものである。

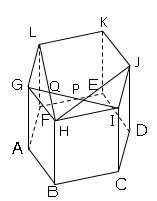
（１）図２に示す立体において、三角錐ＢＨＰＱの体積を求めよ。
（２）図１に示す立体において、点Ｄと点Ｋを結び、線分ＤＫ上に点Ｒを△ＡＤＲと四角形ＢＣＪＧの面積比が１：２となるようにとるとき、線分ＤＲの長さを求めよ。

方針立体の問題は、部分的に取り出して考えるとわかりやすい。

➀
体積を出すので、△ＨＰＱの面積を求める。
また、高さは図よりＨＢとなる。

➀
面積比がでているので、直接面積が求められないか考える。
四角形ＢＣＪＧは台形なので面積が出せる。

➁
△ＡＤＲの面積は面積比より出せる。
ここで四角形ＡＤＫＬと➀の台形は合同だとわかれば、△ＡＤＫの面積がわかる。

➂
△ＡＤＲと△ＡＲＫは高さが共通なので面積比は底辺の比に等しい。これよりＤＲが求まる。

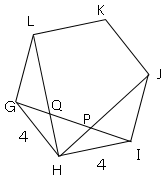
図より、正六角形なので１つの内角は１２０°となる。
また△ＨＧＩはＨＧ＝ＨＩの２等辺三角形となり、他の角度は３０°。
同様に△ＧＨＬ、△ＨＩＪも２等辺三角形となる。
すると∠ＱＨＰ＝６０°となり、ＨＱ＝ＨＰより、正三角形ＨＰＱとなる。

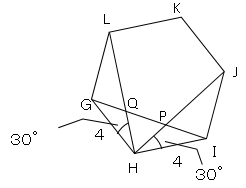
更に∠ＨＧＩも３０°より、△ＨＱＧは２等辺三角形となり、ＧＱ＝ＨＱ、同様にＨＰ＝ＰＩとなる。
よってＧＱ＝ＱＰ＝ＰＩとなる。次にＧＩの長さを求める。

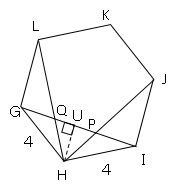
図のように垂線を降ろし交点をＵとすると、△ＨＵＧは３０°、６０°、９０°の特殊な三角形より、
$GU:GH=\sqrt{3}:2$
$GU:4=\sqrt{3}:2$
$GU=2\sqrt{3}$
よって
$GI=4\sqrt{3}$

ゆえに
$QP=\displaystyle \frac{4\sqrt{3}}{3}$
また、ＨＵは
$HU:GH=1:2$
$HU:4=1:2$
$HU=2$
これより△HPQの面積は
$\displaystyle \frac{4\sqrt{3}}{3}×2÷2$
$=\displaystyle \frac{4\sqrt{3}}{3}$
求める体積は

$\displaystyle \frac{4\sqrt{3}}{3}×6÷3$
=$\displaystyle \frac{8\sqrt{3}}{3}$

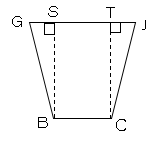
垂線を降ろし交点をＳ、Ｔとする。それぞれの辺を求める。
ＢＧ＝ＣＪなので、片方の長さを求める。
△ＡＢＧに三平方の定理を用いて、
$BG²=AB²+AG²$
$BG²=4²+6²$
$BG=2\sqrt{13}$

次にＧＪの長さを求める。
△ＧＨＪは∠ＧＨＪ＝９０°の直角三角形より、
$GJ²=GH²+HJ²$
$GJ²=4²+(4\sqrt{3})²$
$GJ=8$

次にＧＳの長さを求める。
△ＢＧＳに三平方の定理を用いて、
$BS²=BG²-GS²$
$BS²=(2\sqrt{13})²+2²$
$BS=4\sqrt{3}$
これより、台形ＢＣＪＧの面積は
$(4+8)×4\sqrt{3}÷2$
$=24\sqrt{3}$

面積比より、△ＡＤＲの面積は
$=12\sqrt{3}$

ここで四角形ＡＤＫＬと➀の台形は合同なので、
△ＡＤＫの高さが$4\sqrt{3}$
なので、△ＡＤＫの面積がわかる。
△ＡＤＫの面積は
$8×4\sqrt{3}÷2$
$=16\sqrt{3}$

これより、△ＡＫＲの面積は
$16\sqrt{3}-12\sqrt{3}$
$=4\sqrt{3}$

高さが共通なので底辺の比は
これより
$DR:RK=12\sqrt{3}:4\sqrt{3}$
$DR:RK=3:1$

ゆえに
$DR:DK=3:4$
$DR:2\sqrt{13}=3:4$
$DR=\displaystyle \frac{3\sqrt{13}}{2}$