三平方の定理と影の面積
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
6517 Views
問題１７$1$辺$8cm$の立方体の頂点や辺上の点を結んでできる次の図形$DSFT$の面積を求めよ。
ただし点$S$は辺$AE$の中点、点$T$は辺$CG$の中点とする。
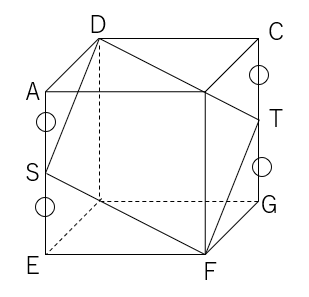
ただし点$S$は辺$AE$の中点、点$T$は辺$CG$の中点とする。
方針
四角形が平行四辺形なのかひし形なのか・・・見分ける。
辺の長さがすべて同じなのでひし形
$DS=SF=FT=DT$
なので求める面積はひし形になります。
ひし形の面積の公式は「対角線×対角線÷２」
よって対角線の長さを求める。
$DF$の長さは立方体の対角線より、
$DF=8\sqrt{3}$
また$ST$の長さは$AC$の長さと同じになる。
よって、三平方の定理より
$AC²=AD²+DC²$
$AC²=64+64$
$AC=8\sqrt{2}$
よって、求める面積は
$8\sqrt{3}×8\sqrt{2}÷2$
$=32\sqrt{6}$
不明点があればコメント欄よりお願いします。