求める体積の出し方を工夫する

問題５

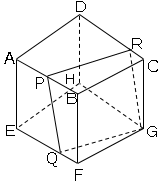
１辺の長さが４ｃｍの立方体ＡＢＣＤ－ＥＦＧＨにおいて、点Ｐは辺ＡＢの中点である。また、点Ｑ，Ｒはそれぞれ辺ＥＦ、ＤＣ上の点であり、ＦＱ＝１ｃｍ、ＣＲ＝１ｃｍである。
このとき、４点Ｐ,Ｑ,Ｇ,Ｃは同一平面上にある。
１、線分ＰＱの長さを求めなさい。
２、線分ＰＧの長さを求めなさい。
３、△ＱＧＲの面積を求めなさい。
４、４点Ｂ,Ｑ,Ｇ,Ｒを頂点をする三角錐の体積を求めなさい。

方針立体の問題は、部分的に取り出して考えるとわかりやすい。

線分ＰＱの長さは３平方の定理より求まる。

線分ＰＧの長さも３平方の定理より求まる。

四角形ＰＱＧＲは４辺が同じなので、ひし形となる。
ひし形の面積の半分が求める面積である。

直接求めることが難しい場合は、他の立体の体積を全体から引くことを考える。

Ｐから線分ＥＦに垂線を引き交点をＩとする。
△ＰＱＩで３平方の定理より、
$PQ²=PI²+IQ²$
$PQ²=4²+1²$
$PQ=\sqrt{17}$

△ＰＢＧで３平方の定理より、
$PG²=PB²+BG²$
$PG²=2²+\sqrt{32}²$
$PG=6$
(ＢＧの長さは△ＢＦＧに３平方の定理を用いて出す。)

よってひし形の面積は
$PG×RQ÷2$
$=6×\sqrt{32}÷2$
$=12\sqrt{2}$
ゆえに求める△ＱＧＲの面積は
$6\sqrt{2}$

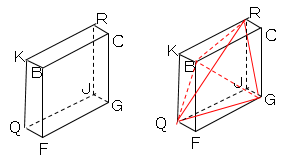
図より求める体積は、
直方体ＢＣＧＦ－ＰＪＫＬから
三角錐Ｋ－ＢＲＱ、Ｆ－ＱＢＧ、Ｃ－ＢＧＲ、Ｊ－ＧＲＱを引けばよい。
（実線に沿って包丁を入れるイメージで考える。）

この４つの体積は皆等しいので、
$((1×4÷2)×4÷3)×4$
$=\displaystyle \frac{32}{3}$
直方体の体積は
$1×4×4$
$=16$
求める体積は
$16-\displaystyle \frac{32}{3}$
$=\displaystyle \frac{16}{3}$