n番目のタイルの個数の問題
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
問題1
図のように白のタイルと黒のタイルを隙間なく規則的に並べて、$1$番目、$2$番目、$3$番目・・・とする。
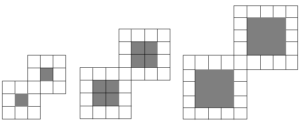
黒のタイルの枚数を$A$、白のタイルの枚数を$B$とする。すると図のような表ができる。

(1)$n$番目の図形について、タイル$A$の枚数とタイル$B$の枚数をそれぞれ$n$を用いて表そう。
(2)タイル$A$の枚数がタイル$B$の枚数より$1043$枚多くなるのは何番目の図形ですか。

マサヤ君
先生これは数えてやってもいいですか?なんかよくわからなくて・・・

土屋先生
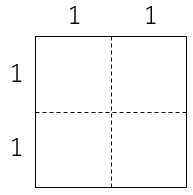
時間があればいいけど・・・(笑)考え方はこうなんだよ。「タイルの個数は面積で考える」と求められることが多いよ。なぜならタイルの面積を求めること$=$タイルの個数を表しているからね。下の図を見てごらん。タイルの枚数は$4$枚$(4=2×2)$になっているね。(正方形の面積の求め方は$1$辺$×1$辺だったね。)これが面積で考えるといい証拠なんだよ。このように理由をつけて考えることがとても大事なんだよ。

マサヤ君
なるほど!学校の数学は公式を使えば何とかなっていたけど、入試問題レベルだとそうもいきませんね。考えることは大事なんですね。

土屋先生
その通りだよ!更にこういう$n$番目を求める式のときは$1$番目と$2$番目、$2$番目と$3$番目のように「前後の数がどのように変化しているか」を考えることが大事だよ。そこからどのように変化していくのか「推測する」力が必要なんだよ~。

ユリコさん
私にもできるかな~?

土屋先生
大丈夫だよ!ここのサイトの問題をたくさん解いて理解すれば平気だよ!

ユリコさん
よ~し。やってみるぞ~

土屋先生
まずは黒のタイルから考えてみよう!

黒のタイルの$1$番目と$2$番目の変化は$2$枚→$8$枚だね。
$1$番目は$1×1$の正方形が$2$個あり全部で$2$個(正方形の面積で求めたよ。)
$2$番目は$2×2$の正方形が$2$個あり全部で$8$個(正方形の面積で求めたよ。)
ここで大事なことは「番目と正方形の$1$辺の長さが同じということ」($1$番目は$1cm$、$2$番目は$2cm$・・・だね。)と「正方形の数は必ず$2$個あること」ってことに気付く。
黒のタイルの$2$番目と$3$番目の変化は$8$枚→$18$枚となる。
$2$番目は$2×2$の正方形が$2$個あり全部で$8$個(正方形の面積で求めたよ。)
$3$番目は$3×3$の正方形が$2$個あり全部で$18$個(正方形の面積で求めたよ。)
ここも同じで「番目と正方形の$1$辺の長さが同じということ」($2$番目は$2cm$、$3$番目は$3cm$・・・だね。)と「正方形の数は必ず$2$個あること」だよ。
ってことは$n$番目も同じはずだね!
「$n$番目と正方形の$1$辺の長さ$(ncm)$が同じ」で「正方形の数は必ず$2$個ある」はずと推測できるね。
$n$番目は$n×n$の正方形が$2$個あり全部で$2n²$個となるよ。

土屋先生
続いて白のタイルの枚数を考えるよ~。どうすればいいかな?

ユリコさん
多分面積で出せると思うけど・・・わかりません(笑)

土屋先生
白のタイルの枚数は全体の枚数から黒のタイルの枚数を引けばいいんだよ。これも大事な考え方だよ。白のタイルを直接求めることができればいいんだけどね。

ユリコさん
てことは白のタイルは全体から黒のタイルを引けばいいんだから・・・
$1$番目は$(3×3)×2-1-2=15$(縦$3cm×$横$3cm$の面積が$2$つあり、重なっている$1$つを引き、黒のタイルを引く)
$2$番目は$(4×4)×2-1-8=23$(縦$4cm×$横$4cm$の面積が$2$つあり、重なっている$1$つを引き、黒のタイルを引く)
$3$番目は$(5×5)×2-1-18=31$(縦$5cm×$横$5cm$の面積が$2$つあり、重なっている$1$つを引き、黒のタイルを引く)
・・・
$n$番目は$(n+2)(n+2)×2-1-2n²$
$=(n²+4n+4)×2-1-2n²$
$=2n²+8n+8-1-2n²$
$=8n+7$

土屋先生
これで(1)の解答がでたね。(2)は(1)を元に考えよう。
タイル$A$の枚数がタイル$B$の枚数より$1043$枚多くなる。
つまりタイル$A$の枚数$=$タイル$B$の枚数$+1043$枚だね。

ユリコさん
タイル$A$の枚数$=$タイル$B$の枚数$+1043$枚だから、
$2n²=8n+7+1043$
$2n²-8n-1050=0$
$n²-4n-525=0$
($525=21,25$だから、$25-21=4$となる。$(x+a)(x+b)=x²+(a+b)x+ab$を使ったよ。)
$(n-25)(n+21)=0$
$n=25$
$25$番目だ!!!!!!

スワンちゃん
因数分解の公式を忘れてたらここから復習だにゃん!
(1)
黒のタイルの枚数は
$1$番目は$(1×1)×2=2$
$2$番目は$(2×2)×2=8$
$3$番目は$(3×3)×2=18$
・・・
よって
$n$番目は$(n×n)×2=2n²$
白のタイルは全体から黒のタイルを引く。
$1$番目は$(3×3)×2-1-2=15$
$2$番目は$(4×4)×2-1-8=23$
$3$番目は$(5×5)×2-1-18=31$
・・・
$n$番目は$(n+2)(n+2)×2-1-2n²$
$=(n²+4n+4)×2-1-2n²$
$=8n+7$
$n$番目の黒のタイルの枚数は$2n²$枚、黒のタイルの枚数は$8n+7$枚となる。
(2)
タイル$A$の枚数がタイル$B$の枚数より$1043$枚多くなるので、
$2n²=8n+7+1043$
$2n²-8n-1050=0$
$n²-4n-525=0$
$(n-25)(n+21)=0$
$n=25$
よってタイル$A$の枚数がタイル$B$の枚数より$1043$枚多くなるのは$25$番目の図形。

土屋先生
➀タイルの個数は面積で求める。
➁番目を求める場合は前後を比較する。
➂あるタイルの枚数は全体から他の部分を引いて求める。

土屋先生
不明点があればLINEもしくは下記コメント欄よりお願いします。







ディスカッション
コメント一覧
めっちゃわかりやすかったです!
ありがとうね(^_-)-☆