素因数分解と因数分解
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
素因数分解
整数がいくつかの整数の積で表されるとき、その1つ1つを因数と呼ぶ。
例
$6=2×3$
その数自身(例の場合は$5$)と$1$のほかに自然数を因数にもたない数を素数と呼ぶ。
※$1$は素数とみなさない。
例
$5=1×5$

素数である因数を素因数と呼び、自然数を素数の積で表すことを素因数分解と呼ぶ。
例
$150$の素因数分解をしましょう。
$150=2×3×5²$
ポイントは「小さい素数」から順に計算していくこと。
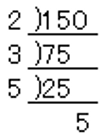
1段目は$150÷2=75$
2段目は$75÷3=25$
3段目は$25÷5=5$
のように割り算をやっていきます。

では問題です。$225$を素因数分解しましょう。
動画で理解しよう!ここまでの内容だよ
因数分解
展開の逆を因数分解と呼び、積の形で表される。
例
$ab+bc$を因数分解しなさい。
$=b(a+c)$
同じものを前に出してかけ算の形を作る。

因数分解の公式
展開の公式の逆になります。
①$x²+(a+b)x+ab=(x+a)(x+b)$
②$x²+2ax+a²=(x+a)²$
③$x²-2ax+a²=(x-a)²$
④$x²-a²=(x+a)(x-a)$
では問題です。次の式を因数分解しましょう。
(1)$x²+5x+4$
(2)$x²+6x+9$
(3)$x²-9$
(4)$x²-6x+9$
工夫する因数分解
例1
$a²x²+x²+2ax²$を因数分解しましょう。
$=x²(a²+1+2a)$(共通因数$x²$でくくる)
$=x²(a²+2a+1)$
$=x²(a+2×a×1+1²)$(➁を使う)
$=x²(a+1)²$

例2
$(a+1)x²-3(a+1)+2x(a+1)$を因数分解しましょう。
$a+1=M$とおく
$=Mx²-3M+2xM$
$=M(x²-3+2x)$(共通因数$M$でくくる)
$=M(x²+2x-3)$
$=M(x+3)(x-1)$(➀を使う)
$=(a+1)(x+3)(x-1)$($M$を元に戻す)
では問題です。次の式を因数分解しましょう。
(1)$(a+b)x-(a+b)y$
(2)$a²b-bc²$
動画で理解しよう!ここまでの内容だよ
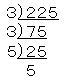











ディスカッション
コメント一覧
まだ、コメントがありません