タイルと数列の関係

問題１５図$1$,図$2$,・・・のように同じ大きさの白と黒の正方形のタイルをある規則で並べて図形を作る。

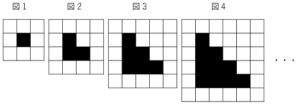
（１）図$5$では、黒のタイルは何枚ですか。
（２）黒のタイルが$91$枚である図では白のタイルは何枚ですか。
（３）白のタイルと黒のタイルの枚数の差が$52$枚である図では、白のタイルは何枚ですか。

方針

（１）

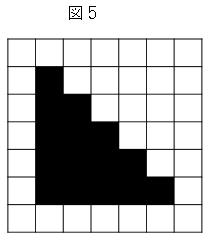
表より黒のタイルは$15$枚

（２）
黒のタイルの法則を考える。
$3$というのは$1$(前の値)に$2$を足したもの。
$6$というのは$3$(前の値)に$3$を足したもの。
$10$というのは$6$(前の値)に$4$を足したもの。
・・・
つまり
$10=6+4$
$10=(3+3)+4$
$10=(1+2)+3+4$
となっていることに気が付くと、

黒のタイルは以下の法則になっている。
$1=1$
$3=1+2$
$6=1+2+3$
$10=1+2+3+4$
$15=1+2+3+4+5$
・・・
$n=\displaystyle \frac{n}{2}(n+1)$
となる。

これは例えば$1$から$10$までの和を求める場合
$1+2+3+・・・+9+10$
$=(1+10)+(2+9)+・・・(5+6)$
ここで()の数は$5$個なので、
$=11×5$
$=55$

これは例えば$1$から$n$までの和を求める場合
$1+2+3+・・・+n-1+n$
$=(1+n)+(2+n-1)+・・・$
ここで$()$の数は$\displaystyle \frac{n}{2}$個なので、
$=\displaystyle \frac{n}{2}(n+1)$

図$n$の黒のタイルの枚数は$\displaystyle \frac{n}{2}(n+1)$
これより白の枚数は$(n+2)²-\displaystyle \frac{n}{2}(n+1)$

黒のタイルが$91$枚なので、
$\displaystyle \frac{n}{2}(n+1)=91$
$n²+n=182$
$n²+n-182=0$
$(n+14)(n-13)=0$
$n=13$

ゆえに白のタイルの枚数は
$(13+2)²-\displaystyle \frac{13}{2}(13+1)$
$=134枚$

（３）
白のタイルと黒のタイルの枚数の差が$52$枚なので、
$(n+2)²-\displaystyle \frac{n}{2}(n+1)$$-\displaystyle \frac{n}{2}(n+1)=52$
$n²+4n+4-n²-n=52$
$3n=48$
$n=16$

ゆえに白のタイルの枚数は
$(16+2)²-\displaystyle \frac{16}{2}(16+1)$
$=188枚$