関数と面積と垂線の関係

問題１１

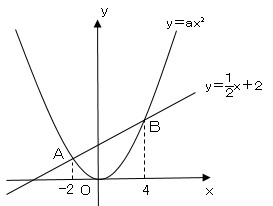
図のように、関数$y=ax²$のグラフと直線$y=\displaystyle \frac{x}{2}+2$が$2$点$A,B$で交わっている。
$2$点$A,B$の$x$座標が、それぞれ$-2,4$である。ただし$a>0$とする。
ア、$a$の値を求めなさい。
イ、△$OAB$の面積を求めなさい。
ウ、原点$O$から直線$y=\displaystyle \frac{x}{2}+2$に垂線$OH$をひくとき、線分$AH$と線分$BH$の長さの比を最も簡単な整数比で表せ。

ア、
点$A$の座標を求める。点$A$の$x$座標が$-2$なので、直線$y=\displaystyle \frac{x}{2}+2$に代入して、
$y=\displaystyle \frac{-2}{2}+2$
$y=1$
$A$の座標は$(-2,1)$となる。これが$y=ax²$上にあるので、
$1=a×(-2)²$
$a=\displaystyle \frac{1}{4}$

イ、
点$B$の座標を求める。点$B$の$x$座標が$4$なので、直線$y=\displaystyle \frac{x}{2}+2$に代入して、
$y=\displaystyle \frac{4}{2}+2$
$y=4$
$B$の座標は$(4,4)$となる。


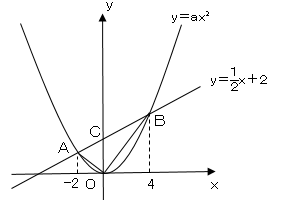
図のように点$C$をおくと△$OAB$の面積は△$OAC$と△$OBC$の面積の和となる。
よって
$2×2÷2+2×4÷2$
$=6$
△$OAB$の面積は$6$

ウ、
線分$AB$の値は
$AB=\sqrt{(4-(-2))²+(4-1)²}$
$AB=\sqrt{6²+3²}$
$AB=\sqrt{45}$
$AB=3\sqrt{5}$


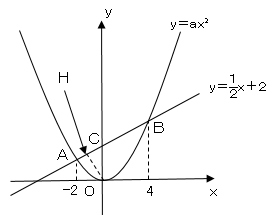
図のように点$H$をおくとイより△$OAB$の面積は$6$なので、
$AB×OH÷2=6$
$3\sqrt{5}×OH÷2=6$
$\sqrt{5}×OH=4$
$OH=\displaystyle \frac{4}{\sqrt{5}}$

$H$の$x$座標を$a$とすると、$y$座標は直線$y=\displaystyle \frac{x}{2}+2$に代入して
$y=\displaystyle \frac{a}{2}+2$

点$H$から$x$軸に垂線を引き、その交点を$D$とする。

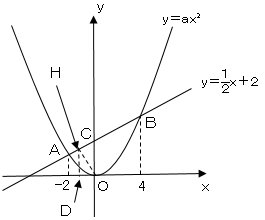
これより三平方の定理より、
$HD²+DO²=OH²$
$(\displaystyle \frac{a}{2}+2)²+a²=\displaystyle \frac{4}{\sqrt{5}}²$
$\displaystyle \frac{a²}{4}+2a+4+a²=\displaystyle \frac{16}{5}$
$\displaystyle \frac{5a²}{4}+2a+4-\displaystyle \frac{16}{5}=0$
$\displaystyle \frac{5a²}{4}+2a+\displaystyle \frac{4}{5}=0$
$25a²+40a+16=0$
$(5a+4)²=0$
$a=-\displaystyle \frac{4}{5}$
これより$H$の$x$座標は$-\displaystyle \frac{4}{5}$

よって$AH:HB$の値は
$-\displaystyle \frac{4}{5}-(-2):4-(-\displaystyle \frac{4}{5})$
$\displaystyle \frac{6}{5}:\displaystyle \frac{24}{5}$
$1:4$
$AH:HB=1:4$