タイルの数と和の関係

問題１６図は黒い正六角形のタイルの周りに数字が書かれた正六角形のタイルを隙間なく配置したものである。ここで$n$と書かれたタイルを「第$n$層のタイル」とあらわす。例、第$1$層は$6$枚、第$2$層は$12$枚である。

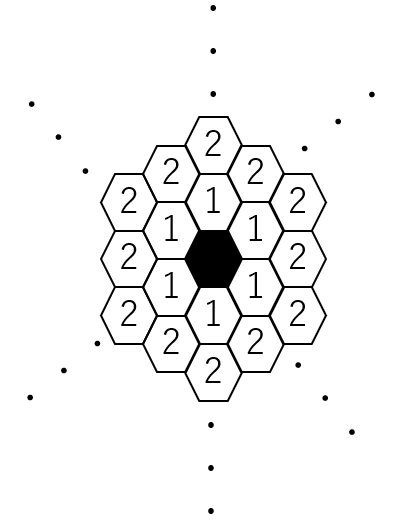
(1)第$5$層のタイルは何枚あるか。
(2)第$n$層のタイルに書かれた数字の合計が$384$の場合、$n$の値を求めよ。
(3)第$m$層のタイルに書かれた数字の合計と第$n$層のタイルに書かれた数字の合計の差が$234$となった。$m$と$n$の組み合わせをすべて求めよ。ただし$m>n$とする。

方針

（１）

これより第$1$層では$6=6×$$1$枚
これより第$2$層では$12=6×$$2$枚
これより第$3$層では$18=6×$$3$枚
・・・
これより第$n$層では$6×$$n$枚

これより第$5$層では$6×5=$$30$枚

（２）
これより第$1$層では$1$が$6$枚で合計は$1$$×6=6$
これより第$2$層では$2$が$12$枚で合計は$2$$×12=24$
これより第$3$層では$3$が$18$枚で合計は$3$$×18=54$
・・・
これより第$n$層では$n$が$6n$枚で合計は$n$$×6n=6n²$

今数字の合計が$384$なので、
$6n²=384$
$n²=64$
$n=8$
よって第$8$層

（３）
$m>n$より、
$6m²-6n²=234$
$m²-n²=39$
$(m+n)(m-n)=39$

$m>n$より、$m-n>0$
これを満たすのは以下になる。
かけて$39$になればよいから
$m+n=39,m-n=1$・・・➀
$m+n=1,m-n=39$(ありえないので不要)
$m+n=3,m-n=13$(ありえないので不要)
$m+n=13,m-n=3$・・・➁
理由は$m,n$ともに正の数なのに、引き算をした数が足し算をした数を上回ることはない。

➀、➁を連立して解いた結果
$m=8,n=5$と$m=20,n=19$