連立方程式と食塩水
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
8850 Views
問題4容器Aには濃度15%の食塩水、容器Bには濃度6%の食塩水がたくさん入っている。次の1~3の操作を行った。
1.容器Aと容器Bから食塩水を取り出して混ぜ合わせて、濃度9%の食塩水300gを作った。
2.容器Aから取り出した食塩水に水160gを混ぜ合わせて濃度9%の食塩水を作った後、それに容器Bから取り出した食塩水を混ぜ合わせて濃度7%の食塩水を作った。
3.1、2で作った食塩水をすべて混ぜた。
1.容器Aと容器Bから食塩水を取り出して混ぜ合わせて、濃度9%の食塩水300gを作った。
2.容器Aから取り出した食塩水に水160gを混ぜ合わせて濃度9%の食塩水を作った後、それに容器Bから取り出した食塩水を混ぜ合わせて濃度7%の食塩水を作った。
3.1、2で作った食塩水をすべて混ぜた。
➀1において、容器Aと容器Bから取り出した食塩水はそれぞれ何gか。
②2において、容器Aと容器Bから取り出した食塩水はそれぞれ何gか。
③3において、混ぜ合わせて得られた食塩水の濃度は何%か求めなさい。答えは少数で表しなさい。
(4)
➀
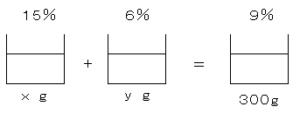
容器Aと容器Bから取り出した食塩水を$xg、yg$とする。
食塩の量=食塩の量で等式を作ると
$x×\displaystyle \frac{15}{100}+y×\displaystyle \frac{6}{100}=300×\displaystyle \frac{9}{100}$・・・①
また食塩水300gを作ったことから
$x+y=300$・・・②
➀を変形して
$15x+6y=2700$・・・③
③-②×6より
$9x=900$
$x=100$
$y=200$
よって容器Aと容器Bから取り出した食塩水は$100g、200g$
②
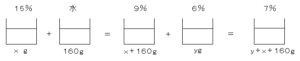
容器$A$と容器$B$から取り出した食塩水を$xg、yg$とする。まずは$x$を求める。食塩の量=食塩の量で等式を作ると
$x×\displaystyle \frac{15}{100}=(x+160)×\displaystyle \frac{9}{100}$
これより
$x=240g$
次に$y$を求める。
食塩の量=食塩の量で等式を作ると
$400×\displaystyle \frac{9}{100}+ y×\displaystyle \frac{6}{100}$
$=(y+400)×\displaystyle \frac{7}{100}$
これより
$y=800g$
よって容器$A$と容器$B$から取り出した食塩水は$240g、800g$
③
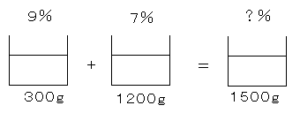
混ぜる前の食塩の量は
$300×\displaystyle \frac{9}{100}+1200×\displaystyle \frac{7}{100}$
$=111g$
よって混ぜた後の食塩水の濃度は
$\displaystyle \frac{111}{1500}×100=7.4$%
➀
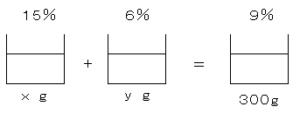
容器Aと容器Bから取り出した食塩水を$xg、yg$とする。
食塩の量=食塩の量で等式を作ると
$x×\displaystyle \frac{15}{100}+y×\displaystyle \frac{6}{100}=300×\displaystyle \frac{9}{100}$・・・①
また食塩水300gを作ったことから
$x+y=300$・・・②
➀を変形して
$15x+6y=2700$・・・③
③-②×6より
$9x=900$
$x=100$
$y=200$
よって容器Aと容器Bから取り出した食塩水は$100g、200g$
②
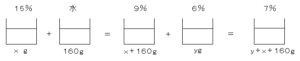
容器$A$と容器$B$から取り出した食塩水を$xg、yg$とする。まずは$x$を求める。食塩の量=食塩の量で等式を作ると
$x×\displaystyle \frac{15}{100}=(x+160)×\displaystyle \frac{9}{100}$
これより
$x=240g$
次に$y$を求める。
食塩の量=食塩の量で等式を作ると
$400×\displaystyle \frac{9}{100}+ y×\displaystyle \frac{6}{100}$
$=(y+400)×\displaystyle \frac{7}{100}$
これより
$y=800g$
よって容器$A$と容器$B$から取り出した食塩水は$240g、800g$
③

混ぜる前の食塩の量は
$300×\displaystyle \frac{9}{100}+1200×\displaystyle \frac{7}{100}$
$=111g$
よって混ぜた後の食塩水の濃度は
$\displaystyle \frac{111}{1500}×100=7.4$%
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません