連立方程式と文章問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
4029 Views
問題５Ａ君は自動車で自宅からｘｋｍ離れたＰ地点までいった。途中のＱ地点までは毎時７０ｋｍの速さで走行し、Ｑ地点で３０分休憩をとった後、毎時４０ｋｍの速さで走行したところ、自宅を出発してＰ地点に到着するまで５時間１８分かかった。また、自宅からＱ地点まではガソリンを１Ｌで１２ｋｍ、Ｑ地点からＰ地点まではガソリン１Ｌで９ｋｍ走ったので、ガソリンの使用量は２３Ｌであった。このときｘの値を求めよ。但し休憩中はガソリンを使用しなかったものとする。
（５）
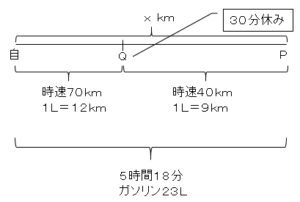
自宅から$Q$地点までの距離を$y$とすると、
時間の関係から
$\displaystyle \frac{y}{70}+\displaystyle \frac{x-y}{40}+\displaystyle \frac{30}{60}=\displaystyle \frac{318}{60}$･･･①
ガソリンの関係から
$\displaystyle \frac{y}{12}+\displaystyle \frac{x-y}{9}=23$･･･②
➀を整理すると
$\displaystyle \frac{y}{70}+\displaystyle \frac{x-y}{40}=\displaystyle \frac{288}{60}$
$\displaystyle \frac{y}{7}+\displaystyle \frac{x-y}{4}=\displaystyle \frac{288}{6}$
$\displaystyle \frac{y}{7}+\displaystyle \frac{x-y}{4}=48$
$7x-3y=1344$･･･③
②×36より
$4x-y=828$･･･④
④×3-③より
$5x=1140$
$x=228$
自宅から$Q$地点までの距離を$y$とすると、
時間の関係から
$\displaystyle \frac{y}{70}+\displaystyle \frac{x-y}{40}+\displaystyle \frac{30}{60}=\displaystyle \frac{318}{60}$･･･①
ガソリンの関係から
$\displaystyle \frac{y}{12}+\displaystyle \frac{x-y}{9}=23$･･･②
➀を整理すると
$\displaystyle \frac{y}{70}+\displaystyle \frac{x-y}{40}=\displaystyle \frac{288}{60}$
$\displaystyle \frac{y}{7}+\displaystyle \frac{x-y}{4}=\displaystyle \frac{288}{6}$
$\displaystyle \frac{y}{7}+\displaystyle \frac{x-y}{4}=48$
$7x-3y=1344$･･･③
②×36より
$4x-y=828$･･･④
④×3-③より
$5x=1140$
$x=228$
不明点があればコメント欄よりお願いします。