比例について
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
比例
ある値($x$の値)が決まると、それに対応する値($y$の値)がただ$1$つに決まることを関数と呼びます。

比例は関数の一部であり、$x$の値が$1,2,3$倍・・・になるにつれて$y$の値も$1,2,3$倍・・・になるものを比例といいます。

比例の式は$y=ax$の形で表されます。($a$のことを比例定数といいます。)

では問題です。毎分$1.5km$の速さで走る列車が$x$分走ると距離は$ykm$進む。$y$を$x$の式で表しましょう。また、これは比例ですか。
変域
変数の取りうる値の範囲を変域といいます。≧,≦,>,<と変数を用いて変域を表します。
例えば、変数$x$を用いて$0$以上$5$以下の変域を表す場合はこのように書きます。$0≦x≦5$

注意:$≦$はこのように分解でき、$<$または$=$になります。なので、$≦,<$の違いはその数を含むか含まないかで、$=$がある、$≦$はその数を含みます。(言葉だと以上、以下になります。)
では問題です。
変数$x$が、次の範囲の値をとるとき、$x$の変域を不等号を使って表しましょう。
(1)$3$以上
(2)$0$以上$5$未満
(3)$-2$より大きく$7$より小さい。
さらにもう一問。
$y$は$x$に比例し、$x=3$のとき、$y=-18$である。
(1)$y$を$x$の式で表しなさい。
(2)$x=-6$のとき$y$の値を求めなさい。
グラフの基礎
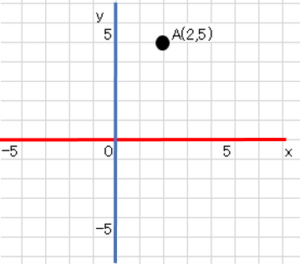
まずはグラフの名称から、赤い線のことを$x$軸、青い線のことを$y$軸といいます。$x$軸,$y$軸の交わった点を原点といい$O$の記号で表す。
例えば、点$A$の座表は以下のように表せる。点$A$は原点より$x$軸の正の方向に$2$, $y$軸の正の方向に$5$動いた点である。これを$A(2,5)$と表す。
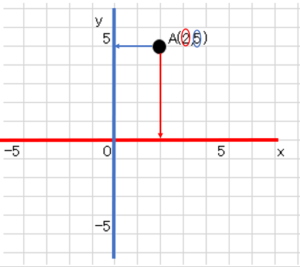
座標を読み取るには上のように考えた方が早いね。点$A$から$x$、$y$軸に垂線を下ろして数字を読み取る。
グラフの書き方
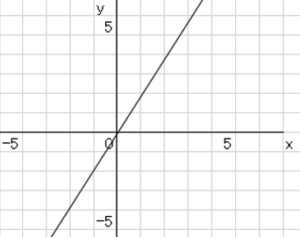
このような図を書くときの手順になります。
➀表を書く。
➁点を書き写す。
➂線で結ぶ。
具体的にやってみましょう。$y=2x$のグラフを書いてみましょう。
➀表を書く。

$x=-3$の場合、$y=2x$に代入して、
$y=2×(-3)$
$y=-6$
これを繰り返して表を埋めると以下の図になる。

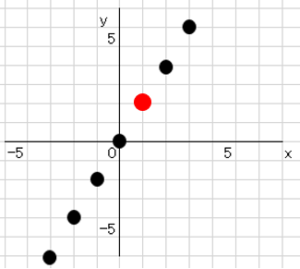
➁点を書き写す。すると、以下の図のようになります。
例として赤い点の場合は表で$x=1,y=2$になります。
➂線で結ぶ。
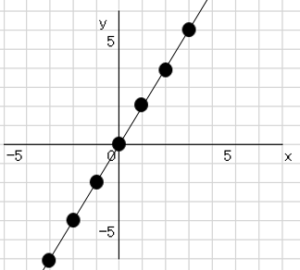
これで$y=2x$のグラフができます。
・・・
でもいちいち書いていたらノートがもったいないです。
じゃあどうやるか。
原点($0,0$)と適当な1点(どこでもいいです)を書き、線で結ぶだけです。
$y=2x$の場合を考えましょう。
$x=1$のとき、$y=2x$に代入すると、$y=2$になる。
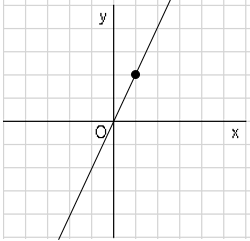

では問題です。$y=\displaystyle \frac{1}{2}x$のグラフを書きましょう。
比例のグラフと式の関係
比例の式$y=ax$の$a$の値について$a>0$の時,$a<0$の時でグラフの向きが変化する。
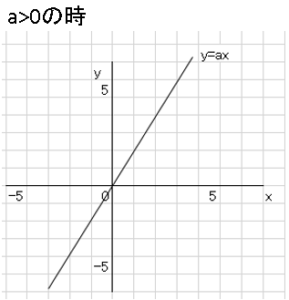
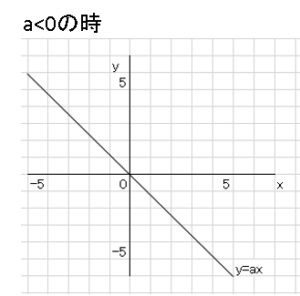
これは覚える必要はありません。具体的に考えてみればよいことです。
$y=2x$のグラフの場合

図より右肩上がりになります。









ディスカッション
コメント一覧
分かりやすい
それはよかったです!
数学のノートのまとめ方
ノートは先生の板書を写すのと、その時に口頭で説明していたことを横に書いておくといいよ