反比例について
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
反比例
反比例は関数の一部であり、$x$の値が２,３倍・・・になるにつれて$y$の値は$\displaystyle \frac{1}{2}$,$\displaystyle \frac{1}{3}$倍・・・になるものを反比例といいます。反比例の式は$y=\displaystyle \frac{a}{x}$の形で表されます。($a$のことを比例定数といいます。ただし、$x=0$は除く)
では問題です。面積が$20㎠$の三角形の底辺を$x㎝$,高さを$y㎝$としたとき$y$を$x$の式で表しましょう。また、これは反比例ですか。
更に問題です。
$y$は$x$に反比例し,$x=-4$のとき$y=9$である。
（１）$y$を$x$の式で表しなさい。
（２）$x=-12$のときの$y$の値を求めなさい。
更にもう一問。次の点を通る反比例のグラフの式をそれぞれ求めましょう。(３,３)
グラフの書き方
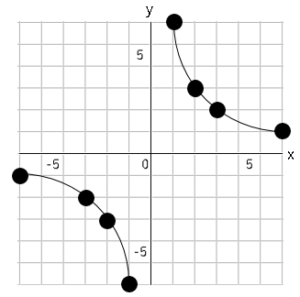
このような図を書くときの手順になります。
➀表を書く。
➁点を書き写す。
➂線で結ぶ。
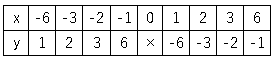
具体的にやってみましょう。$y=\displaystyle \frac{6}{x}$のグラフを書いてみましょう。
➀表を書く。
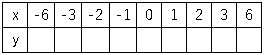
$x=3$の場合、$y=\displaystyle \frac{6}{x}$に代入して、
$y=\displaystyle \frac{6}{3}$
$y=2$
これを繰り返して表を埋めると以下の図になる。
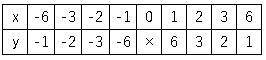
➁点を書き写す。すると、以下の図のようになります。
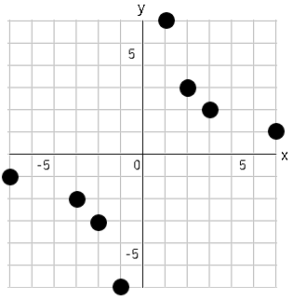
➂線で結ぶ。
これで$y=\displaystyle \frac{6}{x}$のグラフができました。
では問題です。$y=\displaystyle \frac{-6}{x}$のグラフを書きましょう。
反比例のグラフと式の関係
比例の式$y=\displaystyle \frac{a}{x}$の$a$の値について$a>0$の時,$a<0$の時でグラフの向きが変化する。
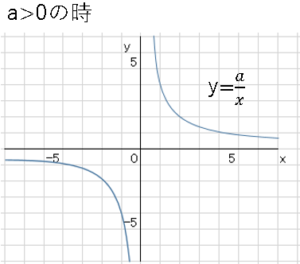
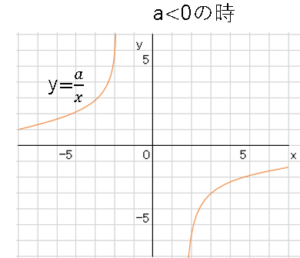
これは覚える必要はありません。具体的に考えてみればよいことです。
$y=\displaystyle \frac{-6}{x}$のグラフの場合
図より左上と右上にグラフがあらわれます。
不明点があればコメントよりどうぞ。