オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
5065 Views
2018年3月16日比例・反比例中学１年生
問１
$y$は$x$に比例し,$x=3$のとき$y=-6$である。$y=-12$のときの$x$の値を求めましょう。
$y$は$x$に比例するので、$y=ax$となる。
$x=3$のとき$y=-6$なので、$y=ax$に代入して、
$-6=3a$
$a=-2$
これより、比例の式は$y=-2x$となる。
$y=-12$のとき$x$の値は、$y=-2x$に代入して、
$-12=-2x$
$x=6$
問２
図のグラフの式を求めましょう。
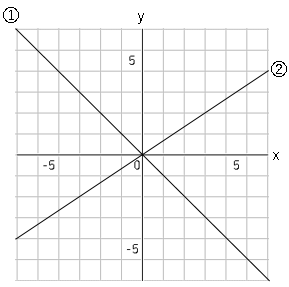
グラフは原点を通り、直線なので比例となる。
比例の式は$y=ax$となる。
➀は$x=1$のとき、$y=-1$を通るので、$y=ax$に代入して
$-1=a$
$a=-1$
これより➀のグラフは
$y=-x$
➁は$x=3$のとき、$y=2$を通るので、$y=ax$に代入して
$2=3a$
$a=\displaystyle \frac{2}{3}$
これより➁のグラフは
$y=\displaystyle \frac{2}{3}x$
問３
点$(b,6)$は、$y=\displaystyle \frac{1}{6}x$のグラフ上にある。$b$の値を求めよ。
$y=\displaystyle \frac{1}{6}x$のグラフ上に、点$(b,6)$があるので、点$(b,6)$を代入して、
$6=\displaystyle \frac{1}{6}b$
$b=36$
問４
点$A(3a+2,5)$、点$B(7,b+8)$がある。点$A$の座標を右に２移動し、下に４移動すると点$B$に重なる。$a,b$の値を求めましょう。
イメージをつかむために、グラフを書く。
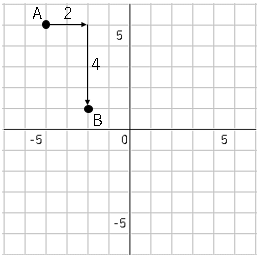
図から点$A$の$x$座標を＋２したら、点$B$の$x$座標に一致する。
図から点$A$の$y$座標を$-$４したら、点$B$の$y$座標に一致する。
これより、以下の式が成り立つ。
$3a+2+2=7$
$3a=3$
$a=1$
$5-4=b+8$
$b=-7$
問５
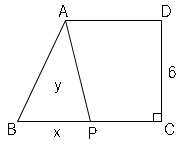
図の台形$ABCD$で、点$P$は辺$BC$上を$B$から$C$まで動く。$BC=9cm$,$CD=6cm$,$BP=xcm$、△$ABP$の面積を$ycm²$とする。
（１）$y$を$x$の式で表そう。
（２）$x,y$の変域を求めよう。
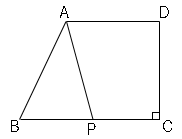
実際に点Pを動かしてみて、面積の移り変わりを確認する。（動点の問題はこれが重要になります。）
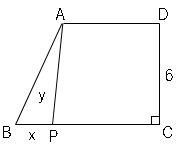
（１）
点$P$をどこに動かそうと高さは変わらない。また底辺は$x$なので、三角形の面積の公式に代入して、
$y=x×6÷2$
$y=3x$
（２）
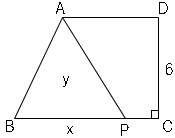
$BP$の長さの$x$は点$P$が点$B$から点$C$まで動くので、
$x$の変域は
$0≦x≦9$
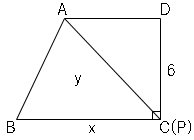
また、面積は点$P$が点Cのときに最大になるので、
最大時の面積は$9×6÷2=27$
これより$y$の変域は
$0≦y≦27$
不明点があればコメントよりどうぞ。