オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
3162 Views
2018年3月16日比例・反比例中学１年生
問１
図で、点$A$は比例$y=\displaystyle \frac{x}{2}$のグラフ上の$x$座標が正である点、２点$B,C$は$x$軸上の点である。四角形$ABCD$が正方形で、点$D$の$x$座標が$28$になるとき、点$B$の$x$座標を求めましょう。
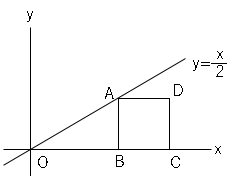
わからないものを文字で置くと色々わかることがある。
点$B$の$x$座標を$b$とすると、点$B$の座標は$(b,0)$となる。
また、点$A$の$x$座標は$b$なので、点$A$の$y$座標は$y=\displaystyle \frac{x}{2}$に代入して
$y=\displaystyle \frac{b}{2}$
これより点$A(b,\displaystyle \frac{b}{2})$
まとめると以下の図のようになる。
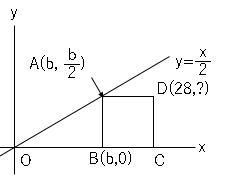
正方形の性質より、$AB=AD$なので以下の方程式が成り立つ。
$\displaystyle \frac{b}{2}=28-b$
$b=56-2b$
$b=\displaystyle \frac{56}{3}$
問２
図で点$A$は比例$y=-2x$と反比例$y=\displaystyle \frac{a}{x}$のグラフが交わる点で、点$P$は原点$O$を出発して毎秒$1cm$の速さで$x$軸上を正の方向に動く点である。点$P$が原点$O$を出発してから$8$秒後の三角形$OPA$の面積が$16cm²$のとき、$a$の値を求めましょう。座標軸の$1$目盛りを$1cm$とする。
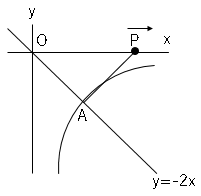
図に色々書きこむと以下の図のようになる。
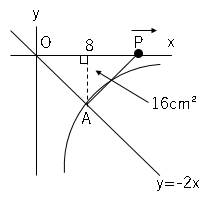
$8$秒後の三角形$OPA$の面積が$16cm²$なので、高さを$x$とすると
$16=8×x÷2$
$x=4$
つまり、点$A$の$y$座標は$-4$
これより、$y=-2x$に代入して、点$A$の$x$座標は
$-4=-2x$
$x=2$
点$A$の座標は$(2,-4)$となる。
点$A$は$y=\displaystyle \frac{a}{x}$のグラフ上なので、
$-4=\displaystyle \frac{a}{2}$
$a=-8$
問３
反比例$y=\displaystyle \frac{150}{x}$のグラフ上で、$x$座標,$y$座標ともに正の整数である点はいくつありますか。
$x=1,2,3,$・・・と代入すると、$y=150,75,50$・・・となることがわかる。
これより、$150$の約数分だけあることがわかる。
$150$の約数は$1､2､3､5､10､15､30､50､75､150$
よって
$10$個
不明点があればコメントよりどうぞ。