関数と座標の関係

問題１９

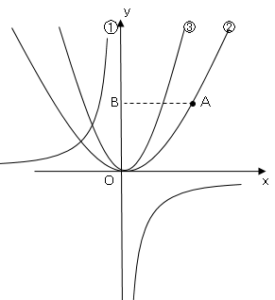
図において、➀は関数$y=\displaystyle \frac{-8}{x}$のグラフ、②は関数$y=\displaystyle \frac{x²}{5}$のグラフ、③は関数$y=ax²$のグラフである。
②のグラフ上に$x$座標が正である点$A$を取り、$A$から$y$軸に垂線を引き、$y$軸との交点を$B$とする。次の問いに答えよ。
(1)関数$y=\displaystyle \frac{-8}{x}$について、$x$の変域が$b≦x≦8$のとき、$y$の変域は$-4≦y≦c$である。$b,c$の値を求めなさい。
(2)③のグラフが、➀のグラフ上の$x$座標と$y$座標がともに整数となる点を通り、線分$AB$と交わるような$a$の値をすべて求めよ。

(1)


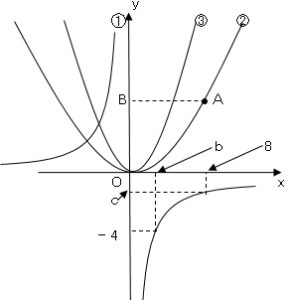
グラフより、$y=\displaystyle \frac{-8}{x}$について、
$-4=\displaystyle \frac{-8}{b}$
$b=2$

$c=\displaystyle \frac{-8}{8}$
$c=-1$

(2)

$a≧\displaystyle \frac{1}{5}$で、➀のグラフが共に整数となる。可能性としてあるのは次の4つである。$(-1,8)、(-2,4)、(-4,2)、(-8,1)$１つずつ確かめると
$8=a×(-1)²$
$a=8$

$4=a×(-2)²$
$a=1$

$2=a×(-4)²$
$a=\displaystyle \frac{1}{8}$

$1=a×(-8)²$
$a=\displaystyle \frac{1}{64}$

これより$a≧\displaystyle \frac{1}{5}$を満たす$a=1,8$が答えとなる。