関数と三角形の面積

問題１８関数$y=ax²$のグラフが、点$A(2,2)$を通るとき、次の問い答えよ。
ア、$a$の値を求めよ。
イ、点$A$を通り、傾きが$-1$の直線の式を求めよ。
ウ、イで求めた直線と関数$y=ax²$のグラフとの交点のうち点$A$とは異なる、点$B$を求めよ。
エ、関数$y=ax²$を動く点$P$がある。点$P$と点$B$を結ぶ直線$BP$と$x$軸との交点を$Q$とする。このとき、△$OPB$と△$OPQ$の面積が共に等しくなるような点$P$の$x$座標を求めよ。ただし、点$P$の$x$座標は正とする。

ア、関数$y=ax²$のグラフが点$A(2,2)$を通るので、
$2=4a$
$a=\displaystyle \frac{1}{2}$

イ、直線の式で傾きが$-1$なので、$y=-x+b$と表すことができる。この直線が$A$を通るので、
$2=-2+b$
$b=4$
よって
$y=-x+4$

ウ、直線と関数が交わるので、
$\displaystyle \frac{1}{2}x²=-x+4$
$x²=-2x+8$
$x²+2x-8=0$
$(x+4)(x-2)=0$
$x=-4,2$
これより点$B$の座標は点$B(-4,8)$これより△$OAB$の面積は
$4×4÷2+4×2÷2$
$=12$

エ、



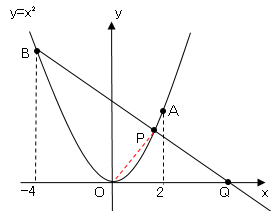
図のようになる。
△$OPB$と△$OPQ$の面積が等しいので、底辺を$PB,PQ$とすると、高さが共通。
ゆえに$PB=PQ$となる。
よって$P$は線分$BQ$の中点となる。
点$P$の$y$座標は
$\displaystyle \frac{8-0}{2}=4$
よって$x$座標は
$4=\displaystyle \frac{1}{2}x²$
$8=x²$
$x=2\sqrt{2}(x>0)$
よって$P$の$x$座標は$2\sqrt{2}$