サイコロと数直線上の問題
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
8184 Views
問題９数直線上に点$P$がある。$1$つのサイコロを投げて、次のルールに従って点$P$が動くものとする。
（ルール）
$1,3,5$の目が出たら、出た目の数だけ正の方向に点$P$を移動させる。
$2,4,6$の目が出たら、出た目の数だけ負の方向に点$P$を移動させる。
最初に点$P$がある位置は数直線上の原点とする。
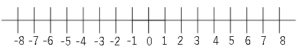
（１）サイコロを$1$回投げた時、点$P$が$3$の位置にある確率を求めましょう。
（２）サイコロを$2$回投げる時、点$P$が$2$の位置にある確率を求めましょう。
（３）サイコロを$2$回投げる時、原点から点$P$までの距離が$3$より小さい位置にある確率を求めましょう。
（ルール）
$1,3,5$の目が出たら、出た目の数だけ正の方向に点$P$を移動させる。
$2,4,6$の目が出たら、出た目の数だけ負の方向に点$P$を移動させる。
最初に点$P$がある位置は数直線上の原点とする。
（１）サイコロを$1$回投げた時、点$P$が$3$の位置にある確率を求めましょう。
（２）サイコロを$2$回投げる時、点$P$が$2$の位置にある確率を求めましょう。
（３）サイコロを$2$回投げる時、原点から点$P$までの距離が$3$より小さい位置にある確率を求めましょう。
方針
サイコロ２個は表を書く。
表を全部埋める。
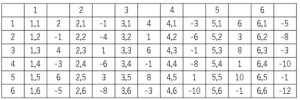
（１）
$\displaystyle \frac{1}{6}$
（２）
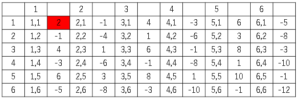
表より$\displaystyle \frac{1}{36}$
（３）
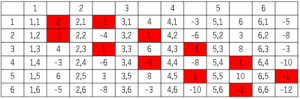
表より$\displaystyle \frac{11}{36}$
不明点があればコメント欄よりお願いします。