関数と交点

問題４図で$n$は$y=ax²(a>0)$のグラフを表す。$A$は$y$軸上の点で、$A$の$y$座標は$1$である。$B$は$n$上の点で、$B$の$x$座標は正である。$ℓ$は$2$点$A､B$を通る直線であり、その傾きは正である。$C$は直線$ℓ$と$x$軸との交点であり、$C$の$x$座標は$B$の$x$座標より$4$小さい。$m$は、$B$を通り傾きが$\displaystyle \frac{1}{2}$の直線である。$D$は直線$m$と$x$軸との交点であり、$D$の$x$座標は$B$の$x$座標より$3$小さい。このとき、$a$の値を求めなさい。

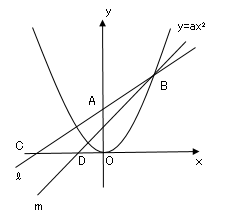
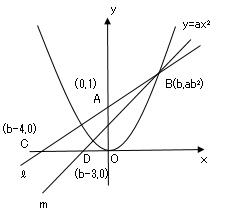
図のように点$B$の$x$座標を$b$とおくと、$y$座標は$y=ax²$に代入して$ab²$となる。
また問題文より点$C,D$の$x$座標は$b-4,b-3$となる。
次に直線$ℓ$の式を求める。
$y=a’x+1$
$0=a'(b-4)+1$
$-1=a'(b-4)$
$a’=\displaystyle \frac{-1}{b-4}$
$y=\displaystyle \frac{-x}{b-4}+1$

次に直線$m$の式を求める。
$y=\displaystyle \frac{x}{2}+b’$
$0=\displaystyle \frac{(b-3)}{2}+b’$
$-\displaystyle \frac{(b-3)}{2}=b’$
$\displaystyle \frac{(3-b)}{2}=b’$
$y=\displaystyle \frac{x}{2}+\displaystyle \frac{(3-b)}{2}$

直線$ℓ,m$を連立させる。
$-\displaystyle \frac{x}{b-4}+1=\displaystyle \frac{x}{2}+\displaystyle \frac{(3-b)}{2}$
$-\displaystyle \frac{b}{b-4}+1=\displaystyle \frac{b}{2}+\displaystyle \frac{(3-b)}{2}$
$-\displaystyle \frac{b}{b-4}=\displaystyle \frac{3}{2}-1$
$-\displaystyle \frac{b}{b-4}=\displaystyle \frac{1}{2}$
$-2b=b-4$
$-3b=-4$
$b=\displaystyle \frac{4}{3}$

直線$m$上に点$B$があるので、
$y=\displaystyle \frac{x}{2}+\displaystyle \frac{(3-b)}{2}$
$ab²=\displaystyle \frac{b}{2}+\displaystyle \frac{(3-b)}{2}$
$a×\displaystyle \frac{16}{9}=\displaystyle \frac{4}{6}+\displaystyle \frac{1}{2}×\displaystyle \frac{5}{3}$
$\displaystyle \frac{16a}{9}=\displaystyle \frac{9}{6}$
$a=\displaystyle \frac{9}{16}×\displaystyle \frac{9}{6}$
$a=\displaystyle \frac{27}{32}$