関数と等積変換
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
2278 Views
問題８関数$y＝2x²$のグラフ上に$2$点$A,B$がある。
点$A$の$x$座標は$-1$,点$B$の座標は$(2,8)$である。
ア、点$A$の$y$座標を求めなさい。
イ、直線$AB$の式を求めなさい。
ウ、関数$y＝2x²$のグラフ上の点で、$2$点$O,B$の間にある点$P$をとると、△$APB$の面積は△$OAB$の面積に等しくなった。
点$P$の座標を求めなさい。但し点$P$は点$O$と異なる点とする。
点$A$の$x$座標は$-1$,点$B$の座標は$(2,8)$である。
ア、点$A$の$y$座標を求めなさい。
イ、直線$AB$の式を求めなさい。
ウ、関数$y＝2x²$のグラフ上の点で、$2$点$O,B$の間にある点$P$をとると、△$APB$の面積は△$OAB$の面積に等しくなった。
点$P$の座標を求めなさい。但し点$P$は点$O$と異なる点とする。
ア、
点$A$の$x$座標は$-1$なので$y＝2x²$に代入し、$y$座標は$y=2$となる。
イ、
直線$AB$を求める。$1$次関数$y=ax+b$に点$A,B$の値を代入
$\begin{equation}\begin{cases}\; 2=-a+b･･･① \\\; 8=2a+b･･･②\end{cases}\end{equation}$
①-②より
$2-8=-a-2a$
$-6=-3a$
$a=2$･･･③
③を①に代入して
$2=-2+b$
$b=4$
これより直線$AB$は$y=2x+4$
点$A$の$x$座標は$-1$なので$y＝2x²$に代入し、$y$座標は$y=2$となる。
イ、
直線$AB$を求める。$1$次関数$y=ax+b$に点$A,B$の値を代入
$\begin{equation}\begin{cases}\; 2=-a+b･･･① \\\; 8=2a+b･･･②\end{cases}\end{equation}$
①-②より
$2-8=-a-2a$
$-6=-3a$
$a=2$･･･③
③を①に代入して
$2=-2+b$
$b=4$
これより直線$AB$は$y=2x+4$
ウ、
△$APB$の面積は△$OAB$の面積に等しくなるので、面積を求めて、点$P$を出しても可能だが、ひと工夫する。
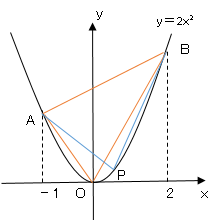
△$APB$の面積と△$OAB$の面積は底辺$AB$を共通にもつ。
つまり高さが等しくなれば良い。
高さを等しくするには、$OP//AB$となればよい。
イより直線$OP$の式は$y＝2x$となる。
これと$y＝2x²$の交点を求める。
$2x²=2x$
$2x²-2x=0$
$2x(x-1)=0$
$x=0,1$
点$P$は点$O$と異なる点なので、$x=1$よって$y＝2$となる。求める点$P$は$(1,2)$
不明点があればコメント欄よりお願いします。