面積と座標の関係

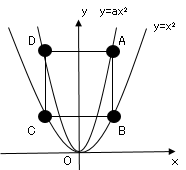
問題３図のように、$2$つの関数$y=ax²(a>1),y=x²$のグラフ上で、$x$座標が$2$である点をそれぞれ$A,B$とする。
また、点$A$を通り$x$軸に平行な直線が、関数$y=ax²$のグラフと交わる点のうち、点$A$と異なる点を$D$とし、点$B$を通り$x$軸に平行な直線が、関数$y=x²$のグラフと交わる点のうち、点$B$と異なる点を$C$とする。
長方形$ABCD$の面積が$24$のとき、$a$の値を求めなさい。

点$C$は点$B$を$y$軸に対象移動させたもので、$x$座標は$-2$となる。
よって$BC=2+2=4$
また、点$A,B$の$x$座標はともに$2$なので、それぞれを$y=ax²,y=x²$に代入する。

点$A$の$y$座標は
$y=a×2²$
$y=4a$
点$B$の$y$座標は
$y=2²$
$y=4$

これより$AB$の長さは$4a-4$、長方形$ABCD$の面積が$24$なので、
$AB×BC＝24$
$(4a-4)×4=24$
$4a-4=6$
$4a=10$
$a=\displaystyle \frac{5}{2}$