関数と面積を二等分する直線

問題７$y=\displaystyle \frac{x²}{4}$のグラフ上に、$3$点$A(-6,9),B(-2,1),C(6,9)$があり、直線$y＝-x＋5$をひいた。
ア、関数$y=\displaystyle \frac{x²}{4}$のグラフと$x$軸に線対称となるグラフの式を求めよ。
イ、直線$y=-x+5$と直線$BC$の交点の座標を求めなさい。
ウ、関数$y=\displaystyle \frac{x²}{4}$で、$x$の変域が$a≦x≦6$のとき、$y$の変域は$0≦y≦9$である。$a$が取ることのできる値の範囲を求めよ。
エ、△$AOC$の面積を$2$等分する$x$軸に平行な直線の式を求めなさい。

ア、
$x$軸に対して対象なので、$y=-\displaystyle \frac{x²}{4}$
イ、
直線$BC$を求める。$1$次関数$y=ax+b$に点$B,C$の値を代入
$\begin{equation}\begin{cases}\; 1=-2a+b･･･① \\\; 9=6a+b･･･②\end{cases}\end{equation}$
①-②より
$1-9=-2a-6a$
$-8=-8a$
$a=1$･･･③
③を①に代入して
$1=-2+b$
$b=3$
これより直線$BC$は$y=x+3$
交点の座標は$1$次関数の交わった点なので、
$-x+5=x+3$
$-2x=-2$
$x=1$
よって
$y=4$

ウ、
図のような範囲にあればよいので$-6≦a≦0$


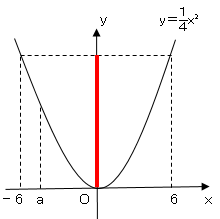
エ、

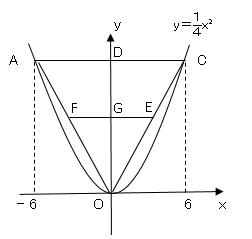
△$AOC$の面積を求める。$AC$と$y$軸との交点を$D$とする。
△$AOC$の面積は
$AC×DO÷2$
$=12×9÷2$
$=27$
△$AOC$の面積を$2$等分する$x$軸に平行な直線との交点を$E,F$とする。

まず、直線$OC$の式を求める。
比例の式で点$C$を通るので、
$y=ax$
$9=6a$
$a=\displaystyle \frac{3}{2}$
よって
$y=\displaystyle \frac{3x}{2}$

$E$の$x$座標を$a$とすると$y$座標は$y=\displaystyle \frac{3a}{2}$また$F$の$x$座標は$-a$となる。

台形$AFEC$の面積を求める。
直線$EF$と$y$軸との交点を$G$とすると台形$AFEC$の面積は
$(AC+EF)×DG÷2$
$=(12+2a)×(9-\displaystyle \frac{3a}{2})÷2$

これが27となるので、
$(12+2a)×(9-\displaystyle \frac{3a}{2})÷2=27$
$(6+a)×(9-\displaystyle \frac{3a}{2})=27$
$(6+a)×(\displaystyle \frac{18-3a}{2})=27$
$(6+a)×(18-3a)=27×2$
$(6+a)×(6-a)=27×2÷3$
$36-a²=18$
$-a²=-18$
$a=3\sqrt{2}$

これより点$E$の$y$座標は
$y=\displaystyle \frac{3×3\sqrt{2}}{2}$
$y=\displaystyle \frac{9\sqrt{2}}{2}$
よって△$AOC$の面積を$2$等分する$x$軸に平行な直線は
$y=\displaystyle \frac{9\sqrt{2}}{2}$